Introduction
Estimating abundance and monitoring changes in population size are critical for the management of harp (Pagophilus groenlandicus) and hooded (Cystophora cristata) seals. Both species have been harvested for centuries in the North Atlantic (Sergeant, 1991; Stenson et al., 1997; Haug et al., 2006; Salberg et al., 2008). There are uncertainties in the assumptions required when estimating seal abundance from catch-at-age data, sequential population models, and mark-recapture data. For this reason, independent estimates of pup production, using aerial photography or visually based strip transect methods, have been recommended and used to determine abundance of both harp and hooded seals in their whelping areas in the northwest Atlantic (Bowen et al., 1987; Hammill et al., 1992; Stenson et al., 1993, 1997, 2002, 2003, 2006), in the Greenland Sea (Øritsland and Øien, 1995; Haug et al., 2006; Salberg et al., 2008) and in the White Sea (Potelov et al., 2003; ICES, 2008). The status of the stocks are subsequently assessed by fitting population models to the independent estimates of pup production (e.g., Healey and Stenson, 2000; ICES, 2006a, 2008; Hammill and Stenson, 2005, 2006, 2007; Skaug et al., 2007). Using aerial surveys in the Greenland Sea, harp seal pup production was assessed in 2002 (Haug et al., 2006) and hooded seals in 2005 (Salberg et al., 2008). Preferably, abundance estimates of hunted seal stocks should be obtained no less than every five years. Surveys and associated data collected more than eight years ago are too old to be considered recent (ICES, 2006a). Therefore, the plan was to conduct new surveys to obtain data necessary for estimation of the abundance of harp seals of the Greenland Sea stock in 2007. However, the historical low pup production estimate obtained for hooded seals in the area in the 2005 survey caused such serious concerns that ICES advised Norway to stop the hooded seal hunt from 2007 and recommended that a new hooded seal survey should be carried out in 2007 (ICES, 2006b). In addition to revisiting all areas historically used by hooded seals for breeding purposes in the Greenland Sea (Salberg et al., 2008), areas to the north and south of the traditional whelping areas were also covered with reconnaissance flights in 2007.
Knowledge of possible variations in the abundance of Greenland Sea hooded seals is rather limited. As judged both from catch per unit effort analyses and mark-recapture pup production estimates, it was assumed that the stock has been increasing since the early 1960s, but evidence of the level of increase has been imprecise (Ulltang and Øien, 1988; Øritsland and Øien, 1995). Aerial surveys to estimate the hooded seal pup production were attempted in the Greenland Sea both in 1959 (Øritsland, 1959; Rasmussen, 1960) and in 1994 (Øritsland and Øien, 1995) but with little success. More successful aerial surveys suggested a minimum pup production estimate of 24 000 (SE = 4 600, CV = 19.0%) in 1997 (ICES, 1998, 1999). New aerial surveys to assess the Greenland Sea hooded seal pup production were conducted in 2005, which resulted in an estimate of the hooded seal pup production of 15 200 (SE = 3 790, CV = 24.9%) pups (Salberg et al., 2008).
A secondary goal for the 2007 survey was to obtain a new abundance estimate for harp seals in the Greenland Sea. As for the hooded seals, available knowledge of the Greenland Sea harp seals abundance is limited. As judged both from catch per unit effort analyses and mark-recapture pup production estimates, the stock appears to have increased since the early 1960s, but evidence of the level of increase has been imprecise (Ulltang and Øien, 1988; Øien and Øritsland, 1995). During the period 1977–1991, about 17 000 harp seal pups were tagged in a mark-recapture experiment in the Greenland Sea (Øien and Øritsland, 1995). Based on this experiment, the 1988 pup production was estimated to be in the range of 53 000 – 69 000 (Øien and Øritsland, 1995). Updates of the mark-recapture based pup production estimates indicated a pup production in 1991 of 67 300 (SE = 5 400, CV = 8.0%) (ICES, 2001). Aerial surveys performed in 1991 suggested a minimum pup production of 55 000 (Øritsland and Øien, 1995). New aerial surveys conducted in 2002 (Haug et al., 2006), yielded an estimate of 98 500 (SE = 16 800, CV = 17.0%).
During the 2007 survey, it proved possible to obtain data on the pup production of both harp and hooded seals in the Greenland Sea. The survey methods were comparable with previous surveys performed for harp and hooded seal assessments. Using the aerial strip transect method (Kingsley et al., 1985), the seal pups are either counted visually along the entire transect strip (which has a known width) flown by helicopter, or on photographs taken along the transect strip using fixed-wing aircraft. Parallel transects are flown in order to sample the entire patch. To extrapolate the counted number of pups on the strips to the number of pups in the whole patch, a conversion factor determined by dividing the transect interval by the transect width is used. This method does not take into account spatial seal density variability along transects, but extrapolates the mean density along a transect to areas between the transects (e.g., Stenson et al., 2003). According to Salberg et al., (2009), the underlying assumption behind the classical way of estimating the variance for this type of surveys is equal mean values between two neighboring transects. This can lead to an overestimate of the variance if the data are highly clustered. For this reason, Salberg et al., (2009) have suggested a new method to estimate the seal pup production, where the expected seal density (or seal counts) in a patch is modeled as a function of spatial position using a General Additive Model (GAM).
In this paper we present results from the 2007 survey carried out in the Greenland Sea. Details of the reconnaissance surveys and the photographic surveys are presented along with the steps involved leading to the final pup production estimate. In addition to estimate the pup production and the uncertainty of the pup production estimate the effect of reader error and correction of pup visibility is considered. When analyzing data from the current survey, both the standard and the new GAM-based method were applied. For further comparison between the two methods we included data from the Greenland Sea 2002 harp seal survey (from Haug et al., 2006) and the Greenland Sea 2005 hooded seal survey (from Salberg et al., 2008).
Material and Methods
The Greenland Sea 2007 harp and hooded seal survey
Reconnaissance surveys. The ice cover was very close to the East Greenland coast in 2007 and surveyed areas were generally over the continental shelf (300–400 m depth). Whelping seals (concentrations as well as scattered seals) were located using fixed-wing and helicopter reconnaissance surveys in the period from 14 March to 3 April in areas historically used by hooded and harp seals, which consisted mainly of pack ice along the eastern coast of Greenland between 66° 55' N 25° 30' W and 75° 30' N 9° 23' W (shaded area in Fig. 1). The reconnaissance flights were adapted to the actual ice configuration during the survey period. Survey altitudes were 160–300 m. Owing to ice drift and a range of pupping dates (mid to late March, Rasmussen, 1960; Øritsland, 1964; Øritsland and Øien, 1995; Haug et al., 2006; Salberg et al., 2008), most areas were surveyed repeatedly to minimize the chance of missing pup concentrations. Colour markers, VHF transmitters and one satellite-based Argos calib were deployed in major whelping concentrations to facilitate relocation and to monitor ice drift (Fig. 2).
Helicopter reconnaissance flights were flown at altitude 200–300 m covering the area between 71° 28'–73° 57' N and 13° 27'–19° 00' W as repeated systematic east-west transects from the ice edge in the east and into more close drift ice (Fig. 1). The lengths of the transects were 10–30 nm and they were generally spaced 5 nm apart, but modified according to the actual ice configuration during the surveys.
The reconnaissance fixed-wing surveys covered the entire area of potential hooded and harp seal whelping in the West Ice (Fig. 1). These surveys were usually flown at altitudes between 200–300 m, but due to low cloud base, for some short periods, surveys were also flown at lower altitudes. Repeated systematic east-west transects normally spaced 10 nm apart were flown from the eastern ice edge and usually 20–30 nm (sometimes longer) over the drift ice to the west. Transects were usually ended in the west when the ice conditions changed to be very dense, with no water between the ice flows, and increasing amount of snow on the ice. Along the eastern ice edge, additional transects were flown in order to cover tongues of drift ice stretching to the east. In areas where seals were concentrated, transects were spaced from 1 nm to 5 nm.
Photographic surveys. Two fixed-wing twin engine Piper Navajo aircrafts (LN-NPZ and LN-NAB) were used to conduct the photographic surveys. The LN-NPZ aircraft was equipped with a Leica RC 30 camera with a motion compensation mechanism shooting AGFA X100 colour film. The camera was fitted with a 15.3 cm lens, and photographic surveys were conducted at altitudes of approximately 250 m (800 ft) for hooded seals and 190 m (600 ft) for harp seals. The LN-NAB was equipped with a Vexcel Ultra Cam D digital camera, which provided multichannel images (Red Green Blue Infrared). The digital camera was operated at altitudes of approximately 310 m (1 000 ft) for both harp and hooded seals. On average the photo coverage was about 100 000 m2 for the analog camera and 50 000 m2 for the digital camera.
To maintain correct altitude, LN-NPZ was fitted with a radar altimeter and LN-NAB was fitted with barometric altimeter. Altitudes based on the GPS navigation systems were logged along the transect lines, and later used to correct the altitudes on all photos. The altitudes on each photo were estimated using bilinear interpolation based on the geoid model EGM96. Correct distances between transects were maintained using GPS.
The helicopter was used to define the geographic range of the whelping patches prior to the fixed-wing aircraft photo surveys. Cameras were turned on when seals were observed on a transect line. Cameras were turned off when the transect line ended at the eastern ice edge, or when no seals were observed for an extended period along the line to the west.
On 27 March, the area between 72° 00' N 18° 35'–16° 49' W and 73° 30' N 15° 40'–13°00' W was photographed using both aircrafts in order to cover the entire area of scattered whelping hooded seals (Patch A in Fig. 1). In the northern parts of the covered area, concentrations of whelping harp seals also occurred. A total of 19 transects spaced 5 nm apart were flown. Two photos per 1 nm were taken along each line, resulting in a total of 1 136 photos (Table 1).
On 29 March, the area between 73° 03' N 15° 42'–14° 42' W and 73° 33' N 15° 20'–13° 50' W was photographed using both aircrafts to cover the largest patch of whelping harp seals (Patch B in Fig. 1). A total of 16 transects spaced 2 nm apart were flown. Both cameras were operated in order to cover 80–90% of the area along each transect line, resulting in a total of 1 987 photos (Table 2).
On 3 April, the area between 71° 22' N 17° 40'–18°00' W and 71° 30' N 17° 27'–17° 46' W was photographed in order to cover the southernmost harp seal whelping patch using LN-NAB (Patch C in Fig. 1). Five transects spaced 2 nm apart were photographed in order to cover 80–90% of the area along each transect line, resulting in a total of 264 photos (Table 3).
Photographic counts. Two experienced readers examined both the negative films and the digital photos. The negative films were examined using a light board in combination with a binocular microscope (type Leica Wild M715) fitted with a lens giving a 6.4–40× magnification. For each photograph the number and position of all pups were recorded on a clear acetate overlay. The digital photos were analyzed using Adobe Photoshop and the positions of all pups were recorded on a digital overlay.
After reading all photographs, the readers re-read a series of their photographs in sequence to determine if identifications had improved over the course of the readings. Photos were read until the second readings were consistently within 1% of the first. The original readings were replaced with the second readings up to this point. Additional photos were read subsequently to ensure that the first and second reading were consistent.
To correct for misidentified pups, a number of photos were selected from one reader and read by the other reader. Then the two readers compared their readings and agreed on the best estimate of the number of pups present on a photograph. We assumed that the “best estimate” (y) was modeled as yj,k = a + bnj,k + uj,k, where nj,k is the counts of the kth photograph in the jth transect, a is the intercept, b is the slope, and uj,k is a random component. The “best estimates” (yj,k) were regressed on the original counts (nj,k) to determine a linear correction model for each photo,

The measurement error for each photo associated with predicting the best estimate given was (Salberg et al., 2008; Kleinbaum et al., 1988)

where 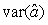 is the variance of the intercept, is the variance of the intercept, 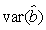 is the variance of the slope, is the variance of the slope, 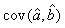 is the covariance between the slope and the intercept, and is the covariance between the slope and the intercept, and 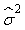 is the estimate of the variance of the random component u. The measurement error for the whole survey is then (Salberg et al., 2008) is the estimate of the variance of the random component u. The measurement error for the whole survey is then (Salberg et al., 2008)

where Wj = lj/Aj, Aj is the area covered of all photographs on transect j, and lj is the length of transect j. The number of transects in the ith survey is denoted Ji, Pij is the number of photos on the jth transect in the ith survey, and Ti is the spacing between transects in survey i.
If the intercept term is not statistically significant on a specified level it should be dropped from the linear correction model. The variance expression is then simplified to
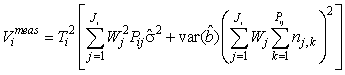
Estimation of abundance
In this section we describe two methods of estimating the pup production and the uncertainty of the pup production estimate. For completeness both methods are described in detail. We have chosen to use the term “conventional survey analysis” for the standard method of analyzing such survey data. This does not mean that this method is the conventional way of analyzing any type of strip transect count data, but rather refers to that this has been the standard method used for analyzing strip transect count data of pups on ice and used in Hammil et al. (1992), Stenson et al. (1993, 1997, 2002, 2003, 2006), Haug et al. (2006), Salberg et al. (2008), and Potelov et al. (2003). The term “conventional survey analysis” refers both to the actual pup production estimator and the method for estimating the uncertainty of the pup production estimate.
Conventional survey analysis. The photographic surveys were based on a systematic sampling design with a single random start and a sampling unit of transects of variable length. The estimated number of pups on the ice at the time of survey for the ith patch may be written as (Salberg et al., 2008)
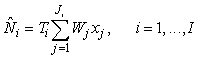
where  is the sum of the corrected counts on transect j, and I is the number of surveys. This estimator accounts for changes in transect width along transects and between transects. is the sum of the corrected counts on transect j, and I is the number of surveys. This estimator accounts for changes in transect width along transects and between transects.
The estimates of error variance 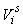 , based on serial differences between transects were calculated as (Salberg et al., 2008) , based on serial differences between transects were calculated as (Salberg et al., 2008)

This estimator assumes that the mean is constant between two neighboring transects. For the seal pup data this assumption is often not valid, and we will have an unwanted contribution from the difference between the transect count mean values which causes an overestimate of the variance of the pup production estimate (Cochran 1977). The variance associated with the mis-identification corrections 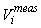 was added to the sampling variance to obtain the variance of a given survey Vi (Stenson et al., 2003, 2006; Haug et al., 2006) was added to the sampling variance to obtain the variance of a given survey Vi (Stenson et al., 2003, 2006; Haug et al., 2006)
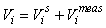
GAM survey analysis. In the survey analysis developed in Salberg et al. (2009) the data was analyzed using spatial modeling methods based on Generalized Additive Models.
Even thought we are dealing with count data, a Poisson error distribution would not be appropriate because the seal count data are over-dispersed. Over-dispersed data are often a consequence of the population being clustered (McCullagh and Nelder, 1989). We therefore assume that the data are negative binomial distributed, which has been applied previous to model over-dispersed count data (Thurston et al., 2000; Hinde and Demétrio, 1998; Gardner et al., 1995; Augustin et al., 1998).
The counted number of pups in the kth photograph is

where Ak is the area covered by the kth photograph, and dk is the density of pups in photograph k. We assume that nk is negative binomial distributed with mean μk, and shape parameter κ. The purpose of the GAM is to model the pup density over the patch as a function of spatial location x = [x1, x2]. Using the logarithmic link function g(μk) = ηk = log(μk), the pup density is modeled as
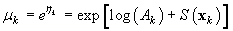
where log(Ak) is an offset variable, and S(·) is a smoothing function of the spatial covariates, and xk is the spatial location at the kth sampling point. Note that the estimated expected seal density is then
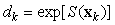
The smoothing function S(x) is modeled using a thin plate regression spline, and the degree of smoothness is determined using generalized cross validation (Wood, 2003). Once the model has been chosen, we may predict the seal density at any location in the patch. Hence, the GAM provides us with a smoothed expected seal density surface over the entire survey area. To estimate the total pup production in the patch, we numerically integrate the expected seal density over space (Augustin et al., 1998; Borchers et al., 1997; Salberg et al., 2009)

where  is the estimated number of pups in the jth fine grid are at spatial location xj. is the estimated number of pups in the jth fine grid are at spatial location xj.
The method used to calculate the variance of the pup production follows exactly the procedures described in detail in Salberg et al. (2009), and has the following compact form

where μg is a vector collecting all fine grid pup density estimates, Xg is the matrix that linearly maps the estimated parameter vector β to the smoothed expected seal density surface. We refer to the original manuscript for a detailed explanation of the various quantities (Salberg et al., 2009).
Pup visibility to aerial surveys
Temporal distribution of births. To correct the estimates of abundance for seal pups that had left the ice or were not yet born at the time of the survey, it was necessary to estimate the distribution of births over the pupping season. This was done by using information on the proportion of pups in each of five distinct age-dependent stages. These arbitrary, but easily recognizable age categories were based on pelage color and condition, overall appearance, and muscular coordination, as described for northwest Atlantic hooded seals by Bowen et al. (1987) and Stenson and Myers (1988), and used in the 2005 survey in the Greenland Sea by (Salberg et al., 2008):
1. Unborn: Parturient females.
2. Newborn: Skin in loose folds along flanks, fur saturated to wet, entire pelage with yellowish hue, awkward body movements. Mother present. Often associated with wet placentas and blood stained snow.
3. Thin blueback: Pup dry, ventrum white, neck well defined, trunk conical in shape. Mother present. Mainly 1–2 days old.
4. Fat blueback: Ventrum white, neck not distinguishable, trunk fusiform in shape. Mother present. Mainly 2–4 days old.
5. Solitary blueback: As in fat blueback, but mother not present. Mainly 4 days or older.
Prior to the survey, classifications of pup stages were standardized among observers to ensure consistency. To determine the proportion of pups in each stage on a given day, random samples of pups were obtained by flying a series of transects over the patch. Pups were classified from the helicopter hovering just above the animals. The spacing between transects depended on the size of the actual patch. Repeated classifications were obtained from each patch several days apart.
A similar procedure was followed for harp seals where information on the proportion of pups in each of seven distinct age-dependent stages was used to assess the temporal distribution of births. These arbitrary but easily recognizable descriptive age categories were based on pelage color and condition, overall appearance, and muscular coordination, as described for the northwest Atlantic harp seals by Stewart and Lavigne (1980):
1. Newborn: Pup still wet, bright yellow colour often present. Often associated with wet placentas and blood stained snow.
2. Yellowcoat: Pup dry, yellow amniotic stain still persistent on pelt. The pup is lean and moving awkwardly.
3. Thin whitecoat: Amniotic stain faded, pup with visible neck and often conical in shape, pelage white.
4. Fat whitecoat: Visibly fatter, neck not visible, cylindrical in shape, pelage still white.
5. Greycoat: Darker juvenile pelt beginning to grow in under the white lanugo giving a grey cast to the pelt, “salt-and-pepper” look in later stages.
6. Ragged-jackets: Lanugo shed in patches, at least a handful from torso (nose, tail and flippers do not count).
7. Beaters: Fully moulted pups (a handful of lanugo may remain).
Estimation of the proportions of pups in each developmental stage were obtained from both hooded and harp seals in both the low-density and high-density areas of seals. The low-density pupping area was covered with systematic east-west staging transects (spaced 2–5 nm apart) on 21, 23, 26, 27 and 28 March, whereas the high-density pupping area was covered with similar transects (all spaced 5 nm apart) on 29 and 30 March (Tables 4 and 5).
Predicted proportion of pups. The temporal distribution of births for both harp and hooded seals was estimated using the method developed in Reed and Ashford (1968) and adapted for modeling the birth distribution for harp and hooded seals in Bowen et al. (1987), and Myers and Bowen (1989). The life cycles of the seals were assumed to be divided into k identifiable age-dependent stages S1, ..., Sk. Birth takes place into state S1 and the pup then progresses in succession through states S1, S2, ... until it attains maturity when reaching state Sk. All pups reaching state Sk eventually die in that state, either from hunting or natural causes (Reed and Ashford, 1968). We assumed that for both seal populations the birth rate could be adequately described by a continuous function of time, m1(t) which denoted the temporal distribution of births. The distribution of births over time was assumed to be a normal distribution with mean value μ1 and standard deviation σ1.
The various development stages are denoted by the subscript j, and a pup passes from stage j to stage j+1. The stage durations are specified in terms of transition intensity functions φj(t), which is the probability that an animal passes from stage j to j+1 in the interval  and has survived. Here and has survived. Here  is the time spent in stage j. The stage duration was assumed to be a semi-Markov process, i.e., the transition intensities depend only on the current stage and the time so far spent in that stage (Bowen et al., 1987). The rate at which pups enter the stage j at time t were denoted by and given by a recurrence relationship (Myers and Bowen, 1989): is the time spent in stage j. The stage duration was assumed to be a semi-Markov process, i.e., the transition intensities depend only on the current stage and the time so far spent in that stage (Bowen et al., 1987). The rate at which pups enter the stage j at time t were denoted by and given by a recurrence relationship (Myers and Bowen, 1989):
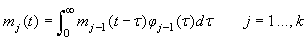
The proportion of pups that will be observed on the ice in stage j at time t is (Bowen et al., 1987, Myers and Bowen, 1989)
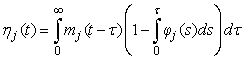
This equation assumes no pup morality and that all pups on the ice are visible. In Bowen et al. (1987, 2007) and Myers and Bowen (1989) the transition intensity functions φj(t) was assumed to follow a Gamma distribution with shape parameter κj and scale parameter ρj for stage j. The product between the shape parameter and the scale parameter, ρj κj, gives the mean duration of stage j.
The numbers of individuals observed to be of stage j at time ti were denoted Sij. The Sij’s were obtained by taking a random sample of the pup abundance and determining the stage of each individual. The predicted proportions of each stage present on time ti , Pij, are calculated as in Myers and Bowen (1989), i.e., by estimating the parameters 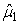 and and 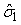 of the birth distribution. The proportion of pups on the ice at time t was estimated using (Salberg et al., 2008) of the birth distribution. The proportion of pups on the ice at time t was estimated using (Salberg et al., 2008)
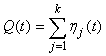
The estimated variance of the proportion of pups on the ice at a given time was estimated by simulating from the proportion of pups in the various stages obtained from the staging by simulating from a multinomial distribution with k stages (Salberg et al., 2008).
Total pup production estimate. To correct for pups still not born, and pups that had left the ice at the time of the photographic survey, the estimated numbers of pups on the ice at the time of the survey were corrected by
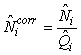
where 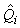 is the estimated proportion of pups visible on the photographs at the time of the survey (as described previously). is the estimated proportion of pups visible on the photographs at the time of the survey (as described previously).
The estimates of Ni and Qi are independent and therefore the error variance of the estimated total number of pups born in the patch 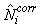 may be obtained using the δ-method, i.e. (Casella and Berger, 1990), may be obtained using the δ-method, i.e. (Casella and Berger, 1990),
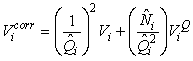
where 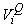 is the estimated variance of is the estimated variance of 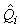 (Salberg et al., 2008). (Salberg et al., 2008).
The total number of pups born was estimated as 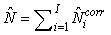 and the error variance was estimated as and the error variance was estimated as 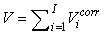 (Salberg et al., 2008). (Salberg et al., 2008).
The Greenland Sea 2002 and 2005 seal surveys
When analyzing data from the current survey, both the standard and the new GAM-based method were applied. For further comparison between the two methods on real data we included data from the Greenland Sea 2002 harp seal survey (from Haug et al., 2006) and the Greenland Sea 2005 hooded seal survey (from Salberg et al., 2008).
Aerial surveys were carried out in March/April 2002 and in March 2005 in the Greenland Sea pack-ice to assess the pup production of harp (2002) and hooded (2005) seals. For the 2002 harp seal data we used photographs from two of the three patches (B and C) to compare the estimates obtained using the conventional and GAM-based methods. Patch A was not photographed but only counted visually. For the 2005 hooded seal data we used photos from all three patches.
Results
Identification of whelping areas
During the period 14–17 March, the helicopter reconnaissance flights covered areas between 71° 28' N and 72° 28' N where only scattered solitary hooded seals (adults and immatures) were observed in the northernmost parts of the area. Scattered family groups of breeding hooded seals were observed during flights on 19 March in areas between 72° 40' N and 73° 05' N. Reconnaissance surveys on 21 and 22 March confirmed the occurrence of scattered hooded seal whelping over a large area between 72° 25' N and 73° 30' N, and an additional survey on 24 March similarly confirmed scattered whelping as far north as to 73° 57' N. No apparent hooded seal whelping concentrations were observed. Only scattered hooded seal “families” and, subsequently, solitary bluebacks over a relatively large area were detected. Staging surveys using the helicopter on 26 and 28 March confirmed this picture and revealed that the main area of scattered hooded seal whelping was between 72° 00' N and 73° 30' N.
After a period (13–20 March) of poor weather conditions, reconnaissance surveys using fixed wing aircrafts were successfully carried out in the period 21 March to 3 April. Nine reconnaissance surveys were flown, covering the eastern parts of the drift ice between approximately 66° 55' N 25° 30' W and 75° 30' N 09° 20' W (Fig. 1). The information obtained from the fixed-wing surveys confirmed observations from the helicopter survey that whelping hooded seals were mainly observed in the area between 72° 00' N 18° 35'–16° 49' W and north to 73° 51'–73° 56' N 14° 25'–13° 45' W. Only a few scattered bluebacks and hooded seal “families” (a total of 19 bluebacks) were observed south of 72° N, mainly in the areas between 71° 20' N 18° 00' W and 72° N 18° 00'–19° 00' W (Fig. 1).
Harp seal pupping was observed in the northeastern part of the scattered hooded seal area, between 73° 15' N and 73° 57' N, during both helicopter and fixed-wing reconnaissance flights in the period 22–27 March. On 28 March, a substantially increased number of harp seals, in a concentrated whelping patch, were observed between 73° 15' N and 73° 40' N. In this patch, staging of harp seal pups was carried out using the helicopter on 29 March. These staging flights also detected scattered hooded seal families and solitary pups (bluebacks) to the west of, and to some extent within, the harp seal patch.
The ice drift varied in the survey period. Based on the satellite calib deployed on the ice, the speed was observed to be up to 15–20 nm per day in a south-southwesterly direction (Fig. 2). It was, therefore, assumed that both the harp seal whelping patch and the scattered hooded seal whelping animals that occurred west of the harp seals, all observed north of 73° 07' N on 29 March, were different seals to all whelping seals observed before that date. A combined reconnaissance and staging survey flown by the helicopter on 30 March confirmed this.
Two small patches of whelping harp seals, which included a few hooded seals, were observed by the fixed-wing aircrafts on 2 April. The smallest patch was located between 72° 23'–72° 24' N 17° 50'–18° 10' W and the second patch was observed further south in the area around 71° 38' N 17° 50' W (Fig. 1).
Temporal distribution of births
Hooded seals. The number of hooded pups in individual age dependent stages for whelping patch A and B are shown in Table 4. No staging data was available for Patch C. The following binning of the various stages of the hooded seal pups were as: stage 1 = Newborn and Thin, stage 2 = Fat, and stage 3 = Solitary.
The parameters used for the transition intensity functions were estimated for hooded seals by Bowen et al. (1987) and were ρ1 = 0.18, and ρ2 = 0.24. Bowen et al. (1987) found the shape parameters to be κ1 = κ2 = 0.86. However, Salberg et al. (2008) observed that these parameters had to be changed to in order to reproduce the results in Bowen et al. (1987). This implied that the mean duration of stage 1 was 1.5 days and the mean duration stage 2 was 2.1 days. In addition we defined stage 3 to have a mean duration of 4 days. The length of stage 3 was assumed to follow a Gamma distribution with the same shape parameter as the distributions for the other stages. Hence the following parameters describe the solitary stage, and κ3 = 8.6.
The estimated parameters of the birth distribution were  (days-in-March) and (days-in-March) and 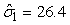 (days). Fig. 3a shows the fit of the model to the proportions observed from the staging survey of Patch A/B for the hooded seals. The fit was fairly good for stage 1 and stage 3. Fig. 3b shows the proportion of hooded pups visible on the ice as a function of time. The estimated maximum proportion of hooded pups on ice was 91.4% on 30 March. On 27 March and 29 March, when the photographic surveys were conducted, the estimated proportions were 71.1% and 88.6%, respectively. The estimated variances of the proportions of total hooded pups visible to the survey in patch A/B were (days). Fig. 3a shows the fit of the model to the proportions observed from the staging survey of Patch A/B for the hooded seals. The fit was fairly good for stage 1 and stage 3. Fig. 3b shows the proportion of hooded pups visible on the ice as a function of time. The estimated maximum proportion of hooded pups on ice was 91.4% on 30 March. On 27 March and 29 March, when the photographic surveys were conducted, the estimated proportions were 71.1% and 88.6%, respectively. The estimated variances of the proportions of total hooded pups visible to the survey in patch A/B were  on 27 March, and on 27 March, and 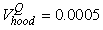 on 29 March. on 29 March.
An unexpected increase of the number of stage 1–2 seals and a decrease in the number of stage 3 seals was observed around 30 March. The cause of this could be a second pulse of births among scattered seals drifting from the north. We expect that the estimates are slightly biased because of this, in the sense that μ1 and are over-estimated. Since a staging survey on 21 March yielded large proportions of thin bluebacks, this estimated birth distribution seemed unlikely.
In order to study the effect of the last staging bout, the model was fitted to the data after removing the observations from 30 March. This change moved the estimate for the maximum births to 23 March, which seemed more likely considering the observed data. The model fit was improved for the remaining observations, and the estimated proportion of seals on ice was increased to 97.7% on 27 March. Using this approach we obtained a very conservative estimate for the proportion of seals on ice for 27 March and no estimate for correcting the counts on 29 March.
Another approach to obtain a better model fit without removing the last staging bout, was to define new values for the mean durations of the various pup stages and calculate new values for the ρj’s. The mean duration of the newborn/thin-stage, and fat stage was increased. The new values for the mean duration of the various stages were: stage 1~2 days, stage 2~3.5 days, and stage 3~4 days. This resulted in the following parameters: ρ1=0.23 days, ρ2=0.41 days and ρ3=0.47 days. The shape parameter for the transition functions was not changed. Using these alternative parameters we obtained a better fit for all stages.
We had no clear reason to believe that a second pulse of births among scattered seals drifting from the north occurred, or that the mean duration of the various stages has been changed. Thus, in the final correction of the estimated pup production the results using the original parameters and the last staging bout on 28 March were used.
Harp seals. The number of pups in individual age-dependent stages for whelping patches A and B are shown in Table 5. No staging data were available for Patch C. We had the following binning of the various stages of the harp seal pups: stage 1 = Newborn, Yellow, stage 2 = Thin, and stage 3 = Fat and Grey.
For the harp seal pups the parameters were estimated in Myers and Bowen (1989) and equal to ρ1=2.32, ρ2=3.31, ρ3=1.71, and a common shape parameter κ=12.7 . It should be mentioned that the parameterization of the Gamma distributions used for the intensity functions are different in Bowen et al. (1987) and Myers and Bowen (1989). The scale parameter used in Bowen et al. (1987) is the ρj and the scale parameter in Myers and Bowen (1989) is 1/ρj. Hence, the mean duration of the stage 1 was 5.5 days, the mean duration stage 2 was 3.8 days, and for stage 3 the mean duration was 7.4 days.
Since we had binned the various harp pup stages slightly different from what had been done in Myers and Bowen (1989), we also had to change the parameters according to our classification of the various stages, namely: stage 1~2.4 days, stage 2~4.42 days, and stage 3~11.39 days. This resulted in the following parameters: ρ1=0.19 days, ρ2=0.37 days, and ρ3=0.92 days. The shape parameter for the transition functions was the same as estimated in Myers and Bowen (1989). The mean durations of the various stages were obtained from Kovacs and Lavigne (1985) and Stenson et al. 2003).
Fig. 4a shows the fit of the model to the proportions observed from the staging survey of Patch A/B for the harp seals. The fit was good around the dates we sampled the staging data. However, it is clear that the staging surveys started too late and were performed too close in time. The estimated parameters of the birth distribution were (days-in-March) and (days). Fig. 4b shows the proportion of harp pups visible on the ice as a function of time. The maximum proportion of harp pups on ice was 98.6% on 26 March. On 27 March and 29 March, when the photographic surveys were conducted, the estimated proportions were 97.5% and 92.3%, respectively. The estimated variances of the proportions of total harp pups visible to the survey in patch A/B were  on 27 March, and on 27 March, and 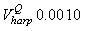 on 29 March. on 29 March.
Correcting of photographic counts
We estimated the parameters using the linear correction model for the various scenarios: digital photos and hooded seals, digital photos and harp seals, analog photos and hooded seals, analog photos and harp seals. For the hooded seals on digital photos we obtained the estimate 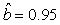 (SE = 0.03) and for analog photos the estimate (SE = 0.03) and for analog photos the estimate 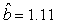 (SE = 0.03). For the harp seals on digital photos we obtained the estimate (SE = 0.03). For the harp seals on digital photos we obtained the estimate 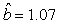 (SE = 0.01) and from analog photos (SE = 0.01) and from analog photos 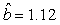 (SE = 0.02). In all cases the intercept term was not statistically significant at the 95% level and were thus dropped from the linear correction model. (SE = 0.02). In all cases the intercept term was not statistically significant at the 95% level and were thus dropped from the linear correction model.
Photographic surveys – conventional method
Patch A. A total of 147 hooded seal pups and 517 harp seal pups were counted on the 1 136 exposures obtained from the 19 transects in the low-density photo survey of Patch A (Table 1). The photoaltitudes for the analog camera in Patch A ranged between 267 m and 315 m, providing coverage ranging from 334×334 m (111 566 m2) to 532×532 m (283 024 m2) per photo. The photo-altitudes for the digital camera in Patch A ranged between 292 and 315 m, providing coverage ranging from 194×292 m (56 648 m2) to 210×315 m (66 150 m2) per photo.
Using the conventional method of estimating the pup production yielded an estimate of 8 535 (SE = 1 083) hooded seal pups and 60 729 (SE = 22 725) harp seal pups. After correcting for the temporal birth distribution and reader error we obtained an estimate of 12 613 (SE = 2 017) hooded seal pups and 66 467 (SE = 24 978) harp seal pups in Patch A.
Patch B. In the high-density coverage of Patch B, 1 987 photos were taken along 26 transects (Table 2). The photo-altitudes for the analog camera in Patch B ranged between 267 and 281 m, providing coverage ranging from 209×209 m (43 681 m2) to 314×314 m (98 596 m2) per photo. The photo-altitudes for the digital camera in Patch B ranged between 267 and 283 m, providing coverage ranging from 178×267 m (47 526 m2) to 189×283 m (53 487 m2) per photo.
A total of 149 hooded seal pups and 1 476 harp seal pups were counted on the photos, resulting in an estimate of 2 876 (SE = 497) hooded seal pups and 34 393 (SE = 9 534) harp seal pups using the conventional estimator for the pup production. After correcting for the temporal birth distribution and reader error we obtained an estimate of 3 347 (SE = 717) hooded seal pups and 41 248 (SE = 11 698) harp seal pups in Patch B.
Patch C. In Patch C, 264 digital photos were taken along five transects (Table 3). The photo-altitudes ranged between 242 and 278 m, providing coverage ranging from 160×241 m (38 560 m2) to 185×278 m (51 430 m2) per photo.
A total of 10 hooded pups and 133 harp seal pups were counted on the photos, resulting in an estimate of 193 (SE = 73) hooded seal pups and 2 867 (SE = 2 140) harp seal pups using the conventional estimator for the pup production. We were not able to correct for the temporal distribution of births since no staging data were available for Patch C. After correcting for reader error we obtained an estimate of 184 (SE = 102) hooded seal pups and 2 811 (SE = 2 263) harp seal pups in Patch C.
All estimates are summarized in Table 6 for the harp and hooded seals.
Total pup production 2007. Combining the estimates obtained for Patch A, Patch B, and Patch C using the conventional method, resulted in a total estimate in the Greenland Sea during the 2007 whelping season of 16 143 (SE = 2 140, CV = 13.3%) hooded seal pups and 110 526 (SE = 27 675, CV = 25.0%) harp seal pups.
Photographic surveys – abundance and uncertainty estimation based on GAMs
The motivation behind applying a GAM-based method for estimating the pup production was to reduce the estimates of the uncertainty of the pup production estimates. Since comparison of the two methods is the aim in this sections, corrections for reader error and correcting for the distribution of births is omitted. Thus, the numbers presented in Table 7 and 8 is the actual estimates obtained from the two methods. The covariates in the GAM model were relative positions of the photos taken. The latitude and longitude coordinates were transformed to a Cartesian coordinates with units in nautical miles. To demonstrate how the estimated densities look like we show the estimated densities for the 2007 hooded seal data in Fig. 5.
In Table 7 estimates are presented for the hooded seal surveys in 2005 and 2007 using both methods. For the 2005 data the pup production was estimated to be 10 718 (SE = 2 380, CV = 22.2%) using the conventional method and 10 836 (SE = 506, CV = 4.7) using the GAM method. For the 2007 data the pup production was estimated to be 11 521 SE = 1 203, CV = 10.4%) using the conventional method and 11 913 (SE = 996, CV = 8.4%) using the GAM method. For both surveys the pup production estimates are virtually the same using both methods. For the 2007 data the variance estimates were close for both methods. However, for the 2005 survey the estimated standard error, and thus also the CV, is much lower using the GAM method.
In Table 8 estimates are presented for the harp seal surveys carried out in 2002 and 2007. For the 2002 data the pup production was estimated to be 132 761 (SE = 25 013, CV = 18.8%) using the conventional method and 135 467 (SE = 7 634, CV = 5.6%) using the GAM method. For the 2007 data the pup production was estimated to be 97 989 (SE = 25 526, CV = 26.0%) using the conventional method and 111 858 (SE = 35 283, CV = 31.5%) using the GAM method. For the 2002 data both methods give similar pup production estimates, but for the 2007 data the difference in the pup production estimates using both methods is large. In addition, the variance estimate is much lower using the GAM method on the 2002 data. For the 2007 harp seal data however, the estimated pup production obtained using the GAM method is much higher than the estimates obtained by the conventional method. We believe the GAM method overestimates the pup production in this case. The reason for this is that the data are zero inflated. The negative binomial or the Poisson model assumption is not an adequate approximation to the conditional distribution of the data (Barry and Welsh, 2002). One possible solution to this could be to model the zero-observations separately as done in (Barry and Welsh, 2002; Borchers et al., 1997).
Discussion
Hooded seals
Surveys using the same methodology (conventional method) as in the present study were conducted to assess the hooded seal pup production in the Greenland Seas in 1997 (ICES, 1999) and 2005 (Salberg et al., 2008). The 1997 pup production was estimated to be 24 000 (SE = 4 600, CV = 19.0%), which was a minimum estimate as it was not corrected for the temporal distribution of births or pups born outside of the whelping patches. The 2005 estimate, corrected both for reader error and the temporal distribution of births, was only 15 250 (SE = 3 473, CV = 22.8%). The most comparable corrected estimate (from the conventional strip transect method) for the 2007 survey was 16 140 (SE = 2 140, CV = 13.3%). Both estimates are still considerably lower than in 1997.
Hooded seals are usually found in lower densities than harp seals (Lavigne and Kovacs, 1988). The accuracy of estimates obtained from aerial surveys is dependent on the degree to which the possible sources of error are minimized. In assessing the relative importance of different sources of bias in estimating seal abundance from aerial surveys, Myers and Bowen (1989) concluded that the greatest source of bias arose from missing whelping concentrations. The extensive reconnaissance surveys conducted in the period 14 March to 3 April of all areas historically used by harp and hooded seals in the Greenland Sea reduced the likelihood of missing major whelping concentrations in 2007. In previous hooded seal surveys, the surveyed areas have traditionally consisted of three strata types: (1) concentrations, i.e., whelping patches, where both visual and photographic surveys were conducted with high-density coverage, (2) scattered pups in areas of historically high pup densities, and (3) scattered pups in areas of historically low pup densities (Bowen et al., 1987; Stenson et al., 1997). For the last two cases, the methodology implied coverage with low-density photographic surveys only. Bowen et al., (1987) observed a considerably lower proportion of scattered pups outside the whelping concentrations in 1984 (17%) than Stenson et al. (1997) in 1990 (43%). In the 2005 Greenland Sea survey hooded seal whelping occurred in three well defined concentrations, but it was not possible to fly an additional low-density coverage survey of scattered pups outside these whelping concentrations (Salberg et al., 2008). Due to this, the total estimate presented was slightly negatively biased. In 2007, all pupping of hooded seals occurred scattered with no major patches of concentrated breeding. The aerial coverage was therefore performed using the low-density coverage method over a large area (Patch A), whereas an additional number of scattered hooded seal pups were surveyed with high-density coverage because they occurred within a dense patch of harp seals (Patch B). When using the low-density coverage method, the transect lines were flown 5 nm apart. A certain possibility that smaller groups/concentrations of pups may have been missed using this approach in the survey area cannot be excluded, although we have no evidence that this occurred.
The calculated pup production estimate was corrected for the temporal distribution of births in Patch A and B. In Patches A and B combined, the maximum percentage of pups on ice occurred on 30 March (91.4%), whereas on the days of the photographic surveys (27 and 29 March) the percentages were 71.1% and 88.0%, respectively. No information about stages was available from Patch C. During the 2005 surveys in the Greenland Sea, the estimated percentages of hooded seals on ice during surveys ranged between 74% and 91% between patches (Salberg et al., 2008), whereas during comparable surveys in the Northwest Atlantic the corresponding percentages were 64% in 1984 (Bowen et al., 1987) and more than 90% in 1990 (Stenson et al., 1997). In the current survey, there was an increase in the proportion of thin/fat as compared with solitary bluebacks on the 30 March staging bout. It is important to note, however, that all staging done in the period 21–28 March included only the scattered pups in Patch A, whereas the staging conducted on 30 March included hooded seal pups scattered in Patch B as well. In previous studies of hooded seal whelping concentrations, it has been observed that the peak of births may vary between patches (Stenson et al., 1997; Salberg et al., 2008). In such cases, separate birth curves are normally fitted to each concentration. If the increased proportion of thin/fat bluebacks in the final staging bout present a signal of more than one pulse of births among the scattered whelping hooded seals in 2007, our fitting of a single unimodal birth curve may have biased the correction of the estimates slightly.
Assuming estimates of pup stage length given by Bowen et al. (1987), results from the staging flights over the whelping patches suggest that the majority of hooded seal females in the Greenland Sea whelped between 23 and 29 March in 2007, peaking on 26 March in Patches A and B combined. This appears to be later (approximately 5 days) than observed in the Greenland Sea in 2005 (Salberg et al., 2008), but similar to observations made in the areas in 1991 and 1994 (Øritsland and Øien, 1995). Both Rasmussen (1960) and Øritsland (1964) suggested the period 15–20 March as the major whelping period for hooded seals in the Greenland Sea.
Changes in the size of harvested seal populations are often attributed to hunting pressure. Although the Greenland Sea stock of hooded seals has been subject to commercial exploitation for centuries (Iversen, 1927; Sergeant, 1966; Nakken, 1988), the hunting pressure has been substantially reduced in the past 2–3 decades (Salberg et al., 2008). However, despite reduced hunting, model runs using recent pup production estimates as input suggest that the Greenland Sea hooded seal population has decreased substantially since the 1950s, and stabilized at a low level (10–15% of the 1946 level) since the 1970s (ICES, 2006b). In other commercially harvested seal stocks in the North Atlantic (hooded seals in the Northwest Atlantic, harp seals in both the Northwest and Northeast Atlantic), models have indicated that reduced catches were followed by population increases from the late 1960s / early 1970s (Hammill and Stenson, 2005, 2006, 2007; ICES, 2006a, b; Skaug et al., 2007). It seems unlikely that the different population development following reduced removals in Greenland Sea hooded seals could have been caused by recent hunting pressure alone. The distributional area of Greenland Sea hooded seals includes virtually all of the Nordic Seas (Greenland, Norwegian and Iceland Sea, Folkow et al., 1996) which are dynamic ecosystems influenced by a combination of factors that will have to be considered simultaneously to explain the observed population development. As recommended by ICES (2006b), future research on Greenland Sea hooded seals should explore possible factors (e.g., reduced fertility, predation, food shortage or disease) that might have contributed to reduce the hooded seal pup production in the area. Such studies are now in progress. Also, potential pupping outside the traditional areas should be explored.
Harp seals
From 1977–1991, about 17 000 harp seal pups were tagged in a comprehensive mark-recapture experiment in the Greenland Sea (Øien and Øritsland, 1995). Based on this experiment, pup production was estimated to be 40 000–50 000 in 1980. Updates of the mark-recapture estimates indicated pup production in 1991 of 67 300 (95% CI 56 400–78 113) (NAFO, 1995). Aerial surveys performed in 1991 suggested a minimum (uncorrected) pup production in this year of 55 000 (CV = 14%) (Øritsland and Øien, 1995). A new aerial survey estimate, obtained in 2002 (98 500. SE = 16 800, CV = 17.9%), suggested that pup production was higher than in 1991 (Haug et al., 2006). The estimate corrected for the temporal distribution of births (from the conventional method) for the 2007 survey was 110 530 (SE = 27 680, CV = 25.0%), i.e., slightly higher than the estimate obtained with comparable methodology in the area five years earlier.
As for previous surveys, extensive reconnaissance surveys were conducted in the period 14 March to 3 April 2007 of all areas historically used by harp and hooded seals in the Greenland Sea, i.e. 67° N and 75° 30' N and both previous (Øritsland and Øien, 1995; Haug et al., 2006; Salberg et al., 2008) and present surveys have confirmed that both species still breed there. However it is difficult to tell if the entire populations were covered on each occasion. There is good evidence to conclude that previous ice conditions in the central Greenland Sea were significantly different from those witnessed in recent decades (Divine and Dick, 2006). These differences manifest themselves as a reduction in extent and concentration of drift ice, particularly within the region around and north of the Jan Mayen island, where the drifting ice traditionally formed an ice-peninsula (Wilkinson and Wadhams, 2005) which used to be an important breeding habitat for harp and hooded seals (Sergeant, 1991). Observed ice reductions may have changed the seal breeding habitat in the Greenland Sea. Could these changes in ice-conditions have triggered behavioral changes of such a magnitude as a relocation of breeding to areas outside those historically known? If so, it is evident that some whelping patches may have been missed by the reconnaissance surveys. The consequence would be pup production estimates that are lower than the actual size of the real pup production of the species occurring in the Greenland Sea. In the 2007 breeding season at least one harp seal whelping patch was observed on the ice in the southernmost parts of Greenland (starting on the southeast side, later driven by the current around the southern tip of Greenland and north on the southwestern side; Rosing-Asvid, 2008). However, results from genetic studies are still not available and therefore it is not known if those seals came from the NW Atlantic or the Greenland Sea. Nevertheless, this could be a warning that parts of the harp seal population have relocated their breeding areas to areas outside those used historically.
The 2007 survey in the Greenland Sea was initially designed to assess the pup production of hooded seals. Thus, the design was adapted to primarily cover the scattered occurrence of hooded seal pups using a low-density coverage method over a very large area (Patch A). This area also contained a whelping concentration of harp seals which was entirely covered and photographed in this low-density coverage survey. Certainly, this is not an optimal way of covering a whelping patch, but due to logistical restrictions, weather conditions and ice drift and dispersal, it proved impossible to cover the harp seal whelping patch located within Patch A with an additional high-density visual or photographic survey. The two other harp seal whelping patches discovered (Patches B and C) were, however, surveyed with high-density photographic coverage. It was not until the survey was well under way that it became evident that the actual localization of breeding patches and scattered pups would permit assessment of both hooded and harp seal pup production. At this point, whelping of the latter had been in progress for several days, resulting in a late start of the staging of harp seal pups. The model fits to the data from Patches A and B were good, but the reason for this could be due to the short intervals (1 day) between staging bouts. No staging data were available from patch C. The estimated proportions of pups present when the photo surveys were conducted were high (>92%) and only small corrections were necessary. Similar observations were made for the primary patch in the 2002 harp seal surveys in the Greenland Sea (Haug et al., 2006) and for most previous harp seal surveys conducted in the Northwest Atlantic (Stenson et al., 2003).
Whereas the Greenland Sea stock of harp seals have been subject to commercial exploitation for centuries, the hunting pressure has been substantially reduced in the past 3–4 decades (Iversen, 1927; Nakken, 1988; Sergeant, 1991; Haug et al., 2006; ICES, 2008). Based on catch per unit effort analyses and mark-recapture pup production estimates, it has been assumed that the population may have increased since the early 1960s, although direct evidence has been limited (Ulltang and Øien, 1988; Øien and Øritsland, 1995). Recent model runs, performed by ICES (2008), have confirmed that the population may have increased in size since ca. 1970, and it has been predicted that the population could continue to increase under the current harvest regime of very small annual removals. The results from the 2007 pup production survey may confirm this.
Assuming that the estimates of the mean and standard deviation of pup stage length were as given by (Kovacs and Lavigne, 1985), results from the staging flights over Patch A and B suggested that the majority of harp seal females in the Greenland Sea whelped between 15 and 21 March in 2007. This was almost identical to the situation observed in 2002 (Haug et al., 2006), and in accordance with observations made in the area in 1991 whereas in 1990 it appears that the breeding may have peaked 5–7 days later (Øritsland and Øien, 1995). Variations from year to year in peak pupping has been observed also for harp seals in the northwest Atlantic where the peak generally occurs earlier than in the Greenland Sea (Stenson et al., 2003). Earlier pupping than in the Greenland Sea is also observed for the White Sea stock of harp seals (Potelov et al., 2003).
Conventional strip transect analysis versus GAM analysis
In Salberg et al. (2008) it was demonstrated that the conventional method for estimating the standard error of the pup production estimate developed in Kingsley et al. (1985) was heavily positively biased when the spatial distribution of the pups were clustered. The bias increased when the degree of clustering increased. The GAM method was developed as an attempt to improve the estimate of the variance of the pup production estimate, and it has been shown that the new method gives lower estimates of the uncertainty of the pup production estimates, even under highly clustered distribution of pups. When the pups were uniformly distributed, both methods performed the same.
The 2007 estimate of the survey precision for hooded seals was SE = 1 203 (CV = 10.4%) using the conventional method, and SE = 996 (CV = 8.4%) using the GAM method, i.e., not very different. The 2005 estimate of the survey precision for hooded seals was SE = 2 380 (CV = 22.2%) using the conventional method, and SE = 506 (CV = 4.7%) using the GAM method. Thus in the 2005 survey the GAM method yielded much lower variance estimate than the conventional method. We believe the reason for this is that the hooded seal pups were almost uniformly distributed in 2007, and under these conditions the underlying assumptions made for the conventional method are met. Hence, the conventional method works under nearly optimal conditions, and under these conditions both estimators should give more or less the same estimates. The 2005 data however, was an example on what can happen when the hooded seal pups occurred very clustered. In this case, the variance estimate was much higher for the conventional method, and we believe that this variance is over-estimated due to the unwanted contribution from the difference between the mean number of pups in to neighboring transects. In addition if we inspect the variance estimates obtained using the conventional method only, it looks as if the pup production estimates obtained in 2007 (CV = 10.4%) are much more precise than those obtained in 2005 (CV = 22.2%). This gives a distorted picture of reality since the photo coverage was much higher for the 2005 survey than for the 2007 survey, and one should therefore expect the survey precision to be better for the 2005 survey. This is better reflected from the estimates obtained using the GAM method with CV = 4.7% for the 2005 data and CV = 8.4% for the 2007 survey.
For the harp seals, the GAM method (CV = 5.6%) gave lower variance estimates than the conventional method (CV = 18.8%) when applied to the 2002 data. We believe that this is due to the effect of clustering of the data. For the 2007 harp seal data however, we saw that the GAM method (CV = 31.5%) provides higher variance estimates than the conventional method (CV = 26.0%). It turns out that the 2007 data contains large number of zero observations, i.e., the large number of photos with no observations of harp pups in the 2007 data. Due to this we experienced that the GAM method was numerically unstable. Dealing with zero inflated data is a known issue for the GAM method and has been reported elsewhere (Barry and Welsh, 2002). The main problem is that the underlying assumption that the counts in the photos are negative binomial distributed is not met. Other distributions, such as the Poisson distribution, were also investigated. Thus, for the 2007 harp seal pup production estimate, the GAM estimate should not be used in its present form.
Analysis of data from the 2002 harp seal survey and the 2005/2007 hooded seal survey show that the two methods give similar estimates of the pup production but the GAM method gives lower estimates of the uncertainty of the pup production estimate. These data sets are examples of what can happen when the data are clustered, in the sense that the conventional method yields positively biased estimates of the uncertainty in the pup production estimates. The 2007 harp seal data show an example of a scenario which is challenging for the GAM method. The GAM method is still under development and we are working on improving the robustness to zero-inflated data. The conventional method is fast, simple and robust to zero-inflated data. However, if the data are clustered it will provide biased estimates of the variance of the pup production estimates.
In general when performing a survey for assessing the pup production one tries to get both counts from aerial photos, and visual counts from flying strip transects using a helicopter. It is rare to have both types of data, but sometimes one might have areal photos of some patches and visual counts of others. Using the conventional method it is straightforward to estimate the pup production based on visual counts. The GAM method need counts within a confined area, such as a photograph. Since the width of the transects flown is known, one solution to this using visual counts could be to bin each transect in a certain length. This would then resemble many photos following each other and the number of pups in each bin is counted. Initial tests of this have been tried out with promising results, but the impact of choosing the bin size need to be explored. A simple way of choosing the bin size could be to try many bin sizes and check whether the pup production estimate stabilizes. Using adaptive bin size, i.e., smaller bin sizes in dense areas, could be another solution.
Since both the GAM-based abundance estimate and the corresponding variance estimate are model dependent, the goodness of fit of the statistical model fitted need to be investigated. Ideally the residuals should be independent and contain no unmodelled spatial correlations. Also, the residual variance should be homogeneous over the patch. If there are substantially unmodelled spatial correlations in the residuals, this may yield negatively biased estimates of the variance (Borchers et al., 1997). Adjusted deviance residuals in Pierce and Shafer (1986) and the randomized quantile residuals developed in Dunn and Smyth (1996) are possible methods to evaluate the goodness of fit of the negative binomial distribution to the count data. The spatial structure of the residuals can be evaluated using the Mantel test (Manly 1997; Granadeiro et al., 2004) to test whether any spatial structure is present in the residuals (Salberg et al. 2009).
Acknowledgements
The authors thank K.-A. Fagerheim, L. Lindblom, N. E. Skavberg, M. Polterman, C. das Neves, pilots, engineers and camera operators, and the crew on board M/S Nordsyssel. Without their assistance and enthusiasm during fieldwork the surveys would not have been completed. We are especially grateful to M. Polterman and L. Lindblom for reading the photos. We thank Garry Stenson and Hans Skaug for useful discussions on issues regarding corrections for reader error. We thank Michael Kingsley for very helpful discussion on both correcting for reader error and details concerning the conventional method. We are very grateful to the anonymous reviewers for all the constructive comments and suggestions that have helped to improve the manuscript.
References
AUGUSTIN, N. H., D. L. BORCHERS, E. D. CLARKE, S. T. BUCKLAND, and M. WALSH. 1998. Spatiotemporal modelling for the annual egg production method of stock assessment using generalized additive models. Can. J. Fish. Aquat. Sci., 55: 2608–2621. doi:10.1139/cjfas-55-12-2608
BARRY, S. C., and A. H. WELSH. 2002. Generalized additive modelling and zero inflated count data. Ecological Modelling, 157: 177–188. doi:10.1016/S0304-3800(02)00194-1
BORCHERS, D. J., S. T. BUCKLAND, I. G. PRIEDE, and S. AHMADI. 1997. Improving the precision of the daily egg production method using generalized additive models. Can. J. Fish. Aquat. Sci., 54: 2727–2742. doi:10.1139/cjfas-54-12-2727
BOWEN, W. D., J. I. MCMILLAN, and W. BLANCHARD. 2007. Reduced population growth of gray seals at Sable Island: Evidence from pup production and age of primiparity. Mar. Mamm. Sci., 23: 48–64. doi:10.1111/j.1748-7692.2006.00085.x
BOWEN, W. D., R. A. MYERS, and K. HAY. 1987. Abundance estimation of a dispersed, dynamic population: hooded seals (Cystophora cristata) in the Northwest Atlantic. Can. J. Fish. Aquat. Sci., 44: 282–295. doi:10.1139/f87-037
CASELLA, G., and R. L. BERGER. 1990. Statistical Inference. Duxbury Press, Belmont, California.
COCRHAN, W. G. 1977. Sampling techniques. 3rd ed. Wiley, New York.
DIVINE, D. V., and C. DICK. 2006. Historical variability of sea ice edge position in the Nordic Seas. J. Geophys. Res., 111: C01001, doi:10.1029/2004JC002851
DUNN, P. K., and G. K. SMYTH. 1996. Randomized quantile residuals. J. Comput. Graph. Statist., 5: 236–244. doi:10.2307/1390802
FOLKOW, L. P., P. E. MÅRTENSSON, and A. S. BLIX. 1996. Annual distribution of hooded seals (Cystophora cristata) in the Greenland and Norwegian Seas. Polar Biol., 16: 179–189. doi:10.1007/BF02329206
GARDNER, W., E. P. MULVEY, and E. C. SHAW. 1995. Regression analysis of counts and rates: Poisson, overdispersed Poisson, and negative binomial models. Psychological Bull., 118: 392–404. doi:10.1037/0033-2909.118.3.392
GRANADEIRO, J. P., J. ANDRADE, and J. M. PALMEIRIM. 2004. Modelling the distribution of shorebirdsin estuarine areas using generalized additive models. J. Sea Res., 52: 227–240. doi:10.1016/j.seares.2004.01.005
HAMMILL, M. O., and G. B. STENSON. 2005. Abundance of Northwest Atlantic harp seals (1960–2005). DFO CSAS Res. Doc. 2005/090, 38 p.
2006. Abundance of Northwest Atlantic hooded seals (1960–2005). DFO CSAS Res. Doc. 2006/068, 23 p.
2007. Application of the precautionary approach and conservation reference points to the management of Atlantic seals. ICES J. Mar. Sci., 64: 701–706. doi:10.1093/icesjms/fsm037
HAMMILL, M. O., G. B. STENSON, and R. A. MYERS. 1992. Hooded seal pup production in the Gulf of St. Lawrence. Can. J. Fish. Aquat. Sci., 49: 2546–2550. doi:10.1139/f92-281
HAUG, T., G. B. STENSON, P. J. CORKERON, and K. T. NILSSEN. 2006. Estimation of harp seal (Pagophilus groenlandicus) pub production in the North Atlantic completed: Results from surveyws in the Greenland sea in 2002. ICES J. Mar. Sci., 63: 95–104. doi:10.1016/j.icesjms.2005.07.005
HEALEY, B. P., and G. B. STENSON. 2000. Estimating pup production and population size of the Northwest Atlantic harp seal (Phoca groenlandica). Can. Stock Assess. Sec. Res. Doc. 2000/081, 28 p.
HINDE, J., and C. G. B. DEMÉTRIO. 1998. Overdispersion: Models and estimation. Comp. Statist. Data Analysis, 27: 151–170. doi:10.1016/S0167-9473(98)00007-3
ICES. 1998. Report of the Joint ICES/NAFO Working Group on Harp and Hooded Seals, ICES Headquarters, 28 Aug.–3 Sept. 1997. ICES CM 1998 / Assess: 35 p.
1999. Report of the Joint ICES/NAFO Working Group on Harp and Hooded Seals, Tromsø, 29 Sept.–2 Oct. 1998. ICES CM 1999 / ACFM: 7, 33 p.
2001. Report of the Joint ICES/NAFO Working Group on Harp and Hooded Seals, ICES HQ, Copenhagen, Denmark, 2–6 October 2000. ICES CM 2001 / ACFM: 8, 40 p.
2006a. Report of the Joint ICES/NAFO Working Group on Harp and Hooded Seals (WGHARP), St.John’s, Newfoundland, Canada, 30 August–3 September 2005. ICES CM 2006 / ACFM: 6, 48 p.
2006b. Report of the Joint ICES/NAFO Working Group on Harp and Hooded Seals, ICES HQ, Copenhagen, Denmark, 12–16 June. 2006. ICES CM 2006 / ACFM: 32, 28 p.
2008. Report of the Joint ICES/NAFO Working Group on Harp and Hooded Seals (WGHARP), Tromsø, Norway, 27–30 August 2008. ICES CM 2008 / ACOM:176, 59 p.
IVERSEN, T. 1927. Drivis og selfangst. Årsber. Vedk. Norges Fiskerier, 1927(2): 1–84 (in Norwegian)
KINGSLEY, M. C. S., I. STIRLING, and W. CALVERT. 1985. The distribution and abundance of seals in the Canadian high Arctic, 1980–82. Can J. Fish. Aquat. Sci., 42: 1189–1210. doi:10.1139/f85-147
KLEINENBAUM, D. G., L. L. KUPPER, and D. E. MULLER. 1988. Applied regression analysis and other multivariate methods. Duxbury Press, Belmont.
KOVACS, K. M., and D. M. LAVIGNE. 1985. Neonatal growth and organ allometry of Northwest Atlantic harp seals (Pagohilus groenlandicus). Can. J. Zool., 63: 2793–2799. doi:10.1139/z85-418
LAVIGNE, D. M., and K. M. KOVACS. 1988. Harps and hoods: Ice-breeding seals of the northwest Atlantic. Universitry of Waterloo Press, Waterloo, 174 p.
MANLY, B. F. J. 1997. Randomization, bootstrap and Monte Carlo methods in biology. 2nd ed. Chapman and Hall, London.
MCCULLAGH, P., and J. A. NELDER. 1989. Generalized Linear Models. Chapman and Hall, London, 2nd ed.
MYERS, R. A., and W. D. BOWEN. 1989. Estimating bias in aerial surveys of harp seal pup production. J. Wildl. Manage., 53: 361–372. doi:10.2307/3801138
NAFO. 1995. Report of the Joint ICES/NAFO Working Group on Harp and Hooded Seals, Dartmouth, Nova Scotia, Canada, 5–9 June 1995. NAFO SCS. Doc. 95/16, 44 p.
NAKKEN, O. 1988. Fangsthistorikk. Fiskets Gang, 74(6/7): 14–15 (in Norwegian).
ØIEN, N., and T. ØRITSLAND. 1995. Use of mark-recapture experiments to monitor seal populations subject to catching. In: Whales, seals, fish and man. A. S. Blix, L. Walløe, and Ø. Ulltang (eds.). Elsivier Science B. V., Amsterdam, p. 35–45.
ØRITSLAND, T. 1959. Klappmyss. Fauna, 12: 70–90 (in Norwegian).
1964. Klappmysshunnens forplantningsbiologi. Fisken Hav., 1964(1): 1–15 (in Norwegian)
ØRITSLAND, T., and N. ØIEN. 1995. Aerial surveys of harp and hooded seal pubs in the Greenland Sea pack ice. In: Whales, seals, fish and man. A. S. Blix, L. Walløe, and Ø. Ulltang (eds.). Elsivier Science B. V., Amsterdam, p. 77–87.
PIERCE, D. A., and D. W. SHAFER. 1986. Residuals in generalized linear models. J. Am. Stat. Assoc., 81: 977–983. doi:10.2307/2289071
POTELOV, V. A., A. P. GOLIKOV, and V. A. BONDAREV. 2003. Estimated pup production of harp seals Pagophilus groenlandicus in the White Sea, Russia, in 2000. ICES J. Mar. Sci., 60: 1012–1017. doi:10.1016/S1054-3139(03)00095-X
RASMUSSEN, B. 1960. Om klappmyssbestanden i det nordlige Atlanterhav. Fisken Hav., 1960(1): 1–23 (in Norwegian).
REED, K. L. Q., and J. R. ASHFORD. 1968. A system of models for the life cycle of a biological organism. Biometrika, 55: 211–221. doi:10.1093/biomet/55.1.211
ROSING-ASVID, A. 2008. A new harp seal whelping ground near South Greenland. Mar. Mamm. Sci., 24: 730–736. doi:10.1111/j.1748-7692.2008.00216.x
SALBERG, A. B., T. HAUG, and K. T. NILSSEN. 2008. Estimation of hooded seal (Cystophora cristata) pup production in the Greenland Sea pack ice during the 2005 whelping season. Polar Biol., 31 : 867–878. doi:10.1007/s00300-008-0425-0
SALBERG, A. B., T. A. ØIGÅRD, G. B. STENSON, T. HAUG, and K. T. NILSSEN. 2009. Estimation of seal pup production from aerial surveys using Generalized Additive Models. Can. J. Fish. Aquat. Sci., 66 : 847–858. doi:10.1139/F09-040
SERGEANT, D. E. 1966. Exploitation and conservation of harp and hooded seals. Polar Record, 12: 541–551. doi:10.1017/S0032247400058757
1991. Harp seals, man and ice. Can. Spec. Publ. Fish. Aquat. Sci., 114: 1–153.
SKAUG, H. J., L. FRIMANNSLUND, and N. I. ØIEN. 2007. Historical population assessment of Barents Sea harp seals (Pagophilus groenlandicus). ICES J. Mar. Sci., 64: 1356–1365. doi:10.1093/icesjms/fsm118
STENSON, G. B., M. O. HAMMILL, M. C. S. KINGSLEY, B. SJARE, W. G. WARREN, and R. A. MYERS. 2002. Is there evidence of increased pup production in northwest Atlantic harp seals, Pagophilus groenlandicus? ICES J. Mar. Sci., 59: 81–92. doi:10.1006/jmsc.2001.1129
STENSON, G. B., M. O. HAMMILL, J. LAWSON, and J. F. GOSSELIN. 2006. 2005 Pup production of hooded seals, Cystophora cristata, in the Northwest Atlantic. Can. Sci. Adv. Sec., Res. Doc., No. 2006/067.
STENSON, G. B., and R. A. MYERS. 1988. Accuracy of pup classifications and its effect on population estimates in the hooded seals (Cystophora cristata). Can. J. Fish. Aquat. Sci., 45: 715–719. doi:10.1139/f88-086
STENSON, G. B., R. A. MYERS, M. O. HAMMILL, I.-H. NI, W. G. WARREN, and M. C. S. KINGSLEY. 1993. Pup production of harp seals, Phoca groenlandica, in the Northwest Atlantic. Can. J. Fish. Aquat. Sci., 50: 2429–2439. doi:10.1139/f93-267
STENSON, G. B., R. A. MYERS, I.-H. NI, and W. G. WARREN. 1997. Pup production and population growth of hooded seals (Cystophora cristata) near Newfoundland, Canada. Can. J. Fish. Aquat. Sci., 54 (Suppl. 1): 209–216. doi:10.1139/cjfas-54-S1-209
STENSON, G. B., L.-P. RIVEST, M. O. HAMMILL, J. F. GOSSELIN, and B. SJARE. 2003. Estimating pup production of harp seals, Pagophilus groenlandicus, in the Norhtwest Atlantic. Mar. Mamm. Sci., 19: 141–160.
STEWART, R. E. A., and D. M. LAVIGNE. 1980. Neonatal growth of northwest Atlantic harp seals (Pagophilus groenlandicus). J. Mammol., 61: 670–680. doi:10.2307/1380312
THURSTON, S. W., M. P. WAND, and J. K. WIENCKE. 2000. Negative binomial additive models. Biometrics, 56: 139–144. doi:10.1111/j.0006-341X.2000.00139.x
ULLTANG, Ø., and N. ØIEN. 1988. Bestandsutvikling og status for grønlandssel og klappmyss. Fiskets Gang, 74: 8–10 (in Norwegian).
WILKINSON, J. P., and P. WADHAMS. 2005. A method of detecting change in the ice conditions of the central Greenland Sea by the whelping locations of harp seals. J. Climate, 18: 1216–1226. doi:10.1175/JCLI3325.1
WOOD, S. N. 2003. Thin plate regression splines. J. R. Soc. Ser. B. Method., 65: 95–114. doi:10.1111/1467-9868.00374
|