Introduction
The Atlantic surfclam, Spisula solidissima, sustains one of the largest shellfish fisheries on the east coast of the U.S. The fishery is operated under a fixed quota distributed to shareholders under an ITQ (individual transferable quota) system (Adelaja et al., 1998; McCay et al., 2011). Surfclams are sensitive to bottom water temperatures above about 21°C (Weinberg, 2005; Munroe et al., 2013). As a consequence, warming of the Mid-Atlantic Bight (Scavia et al., 2002; Jossi and Benway, 2003; Narváez et al., 2015) has resulted in a range contraction for this species since the mid-1990s (Weinberg et al., 2002, 2005; Weinberg 2005) characterized by a large-spatial-scale mortality event at the southern boundary of the range (Kim and Powell, 2004; Narváez et al., 2015) driving the southern boundary northward and offshore. A compensatory northward shift at the leading edge has not occurred, although a modest offshore range extension off New Jersey is well-documented (e.g., Weinberg et al., 2005). A consequence of this shift in range is a contraction of the region supporting much of the fishery from the southern region off Maryland and Virginia to the more northerly region off New Jersey (NEFSC, 2013).
Obvious impacts on the fishery from this range contraction include the movement of processing plants northward, the shift of vessels from southerly ports northward, and the focus of heaviest fishing pressure in a smaller region. These dynamics, both economic, managerial, and biological, influenced the development of a management strategy evaluation (MSE) model of the surfclam industry (see Mahévas and Pelletier, 2004; Baudron et al., 2010; Bastardie et al., 2010; Miller et al., 2010 for other examples of MSE models). One of the dynamic aspects of this evaluation is the need to understand how differences in vessel characteristics and locations of homeports interact with behavioral choices made by captains in determining the degree of success of fishing trips. The approach to fishing implemented by the fleet captains is an important ingredient in the dynamic of any fishing industry (Dorn, 1998, 2001; Gillis et al., 1995a,b; Powell et al., 2003a,b). How these choices interact with changing dynamics of the stock and differences in fishing vessel size represent both an important component of the economic response by the fishery (Lipton and Strand, 1992) and an important component of an MSE. The purpose of this contribution is to utilize an MSE model for surfclams as a vehicle to investigate how ongoing climate change inducing a change in geographic distribution of the stock influences the success of the fishery as modulated through the range of choices potentially available to the vessel captains as they execute their fishing trips.
The Model - SEFES (Spatially-explicit Fishery Economics Simulator)
Overview
SEFES is a model capable of simulating a spatially and temporally variable resource (in this case, surfclams) harvested by fleets of boats landing in a number of homeports. The structure of SEFES is depicted in Fig. 1.
Boats and processing plants are the active agents in the model. The boats are attached to specific processing plants and land catch at dedicated ports. The boat may have varying characteristics such as different speeds, harvest capacities, and costs. Each boat is controlled by a captain with specified characteristics that determine where and how efficiently the boat harvests the resource. SEFES is relatively unique in permitting each captain and vessel to identify a new fishing location for each trip based on specified vessel, behavioral, and stock characteristics (see Bockstael and Opaluch, 1983; Béné, 1996; Hutton et al., 2004 for examples of other models including behavioral choice). Boats move around the domain and harvest clams based on decisions by the captain as constrained by the operating characteristics of the boat, such as speed, maximum allowed time at sea, and imposed harvest quota. Each port has a processing plant that purchases the harvested clams, providing income for the boats, and distributes quota to each boat on a weekly schedule.
The spatial domain is partitioned into rectangular cells ten minutes (about 10 nautical miles (nm) in the modeled region) on a side. Within each cell, the surfclam population is described in terms of surfclams m-2 per 1-cm size class. The number and size distribution of surfclams is modified over time in response to different biological and fishery processes. Surveys are conducted annually to determine the size and distribution of the population. A management module imposes reference points and calculates the allowable biological catch (ABC) used to set the harvest quotas for the next year.
The basic units in the model are SI with time in seconds, distance in meters, and weight in kilograms. For convenience, commonly-used units are used to set various characteristics, such as specifying boat speed in knots (kt). Calendar software is included to convert model days to calendar dates (Julian days). This capability allows the model to determine the beginning of a month or a year and to determine the day-of-the-week for a given event. Being able to identify the month allows the model to impose known seasonal variability such as weather and surfclam yield (meat weight for a given clam length). Being able to identify the day of the week permits fishing trips to be organized with respect to known processing schedules of the processing plants. The length of a simulation is controlled by a start and end calendar date. For these simulations the first day is set arbitrarily at 1 January 2000 and the end date is set arbitrarily at 1 January 2051 which gives a 51-year simulation (2000–2050).
Domain and Geometry Configuration
The model domain is a rectangular distribution of square cells 10 minutes of latitude by 10 minutes of longitude (Fig. 2).
The north-south size of the cell is 10 nm. The east-west size of the cell is fixed at some width determined by the central latitude of the grid. The domain investigated in this paper is the Mid-Atlantic Bight (MAB) off the east coast of the US. The east-west extent of the domain has 17 cells across-shelf in the south and alongshore in the north to represent the transition from a quasi north-south trending shoreline south of Hudson Canyon to an east-west shoreline north of it. The north-south extent of the domain has 26 cells from Long Island south. The central latitude for these cases is 38ºN. For convenience, this model domain has the MAB rotated slightly counterclockwise to remove the northeastward trend south of Long Island, but this slight distortion of the domain has a negligible effect on model processes. Thus, the basic domain is a 17 cell by 26 cell grid wherein each cell is identified by a pair of numbers (ix, iy) which count the number of cells eastward (ix) and northward (iy) from the southwest corner of the model grid.
A mask is imposed on the model domain which identifies each cell as being land, water uninhabited by surfclams, or water inhabited by surfclams. This mask is static, being defined at the beginning of a simulation. Ports are specified to be in certain land cells. For convenience, processing plants and ports are colocated. For the simulations in this paper, four ports are included in the approximate locations of Norfolk, Virginia; Ocean City, Maryland; Atlantic City, New Jersey; and Pt. Pleasant, New Jersey (Fig. 2). These ports represent the primary ports for landing surfclams over the time period of interest. In the 2000s, the majority of the harvest in the Mid-Atlantic Bight was landed in the ports of Atlantic City and Pt. Pleasant. In the 1990s, the Ocean City port was also important and, earlier in the fishery (1980s), the port of Norfolk was important. NEFSC (2003, 2013) show the distribution of landings over time, including the northward shift in effort that resulted in the sequential closure of the Norfolk and Ocean City homeports.
Boat Details
Operational Limits
Activity by boats is monitored hourly. Boats are permitted three activities. They can wait at the homeport, steam to and from a fishing location, or fish. At the beginning of every hour, the current activity of the boat is determined, some action occurs, and an activity for the next hour is set. These actions are managed by three hour counters: HomeWait, TripTime, and FishTime (Table 1). As an action begins, these counters are set to the correct value for a boat to 1) wait at the dock for an opportunity to go fishing, 2) steam from the port to the fishing location or return, or 3) fish.
Operating Characteristics
Vessel characteristics were obtained from interviews in 2012 with industry representatives and boat owners and operators. Although a spectrum of detailed differences exist among vessels in the surfclam fleet, these vessels can be grouped crudely into small (~40-cage capacity), medium (~80-cage capacity), large (~120-cage capacity), and jumbo (~160-cage capacity). For this study, two common vessel types were compared, small and large. The large vessel has 3 times the capacity of the small vessel. Simulations were run with an equivalent fishing power for each port and vessel type. Accordingly, all ports had the same number of vessels of a given size and simulations using small vessels used three times as many small vessels as large vessels. Total fishing power in the simulations was similar to that observed in today’s Mid-Atlantic Bight fishery. Thus, 20 large vessels, five per port, and 60 small vessels, 15 per port, were specified.
Each boat in the model has a number of characteristics set at the beginning of the simulation. The following characteristics were specified for the small vessel: steaming speed, 8 kt; maximum on-deck processing capacity, 6 cages hr-1; dredge width, 2.6 m; dredging speed, 3 kt. The same characteristics for the large vessel were: steaming speed, 12 kt; maximum on-deck processing capacity, 20 cages hr-1; dredge width, 3.8 m; dredging speed, 3 kt.
Boat Economics
Each boat is given a homeport where catch is landed and derives quota from a specified processing plant colocated for convenience at that homeport. Vessel economic data were obtained from MAFMC (1988; see also Weninger and Strand, 2003) and updated by interviews in 2012 with industry representatives and vessel operators. Costs for certain activities are calculated in terms of fuel used and crew costs. Fixed costs of boat and gear maintenance as well as capital costs of the boat are included. For these simulations, the following were specified (small vessel, large vessel): fixed costs ($1,579 d-1, $1,165 d-1); crew share as fraction of catch revenue (0.2, 0.2); boat share as fraction of catch revenue (0.15, 0.15); gear maintenance ($1,500 trip-1, $1,000 trip-1); fuel use steaming (30 gal hr-1, 50 gal hr-1); fuel use fishing (45 gal hr-1, 80 gal hr-1). Note that the higher fuel use while fishing occurs because these vessels use hydraulic dredges and the water pump is engaged while dredging. Note that the higher fixed costs and costs of gear maintenance for the smaller vessels incorporate the average older age of the vessel in service. For these simulations, the ex-vessel value of landings was set at $12 (surfclam bu)-1 and the price of fuel was set at $4 gal-1. As many of the economic values used are temporally variable, economic results are best assessed on a relative basis by comparing outcomes between ports, vessel sizes, and captains.
Captain Descriptors
Information describing a captain’s decision-making process when planning a fishing trip, constraints imposed by landing deadlines, and the captain’s approach to information acquisition on clam abundance were obtained from interviews of vessel captains supplemented by interviews with other industry representatives and the authors’ own extensive experiences.
Captain’s Memory
The captain controls where the boat fishes. Each captain retains the memory of past fishing trips which influences which 10-minute square is targeted for the next fishing trip. This memory log contains an expected LPUE (landings per unit effort) specified in cages per hour fishing for every fishable 10-minute square in the domain. At the beginning of the simulation, the memory of each captain contains the LPUE that would be experienced by his boat for all 10-minute squares based on the square’s initial surfclam abundance. That is, initially, all captains have omniscient information. At the end of each fishing trip, the catch history in the captain’s memory log is updated for that 10-minute square. In this way the captain’s memory of the entire domain degrades over time as the surfclam population changes independently of the captain’s experience and, therefore, updated memory of it. The captain uses his memory of LPUE to choose a 10-minute square for fishing.
Each captain has a memory weight factor that is used to update the memory log. After fishing in a certain 10-minute square and returning to port, the LPUE for that trip is used to update the information in the captain’s memory log based on a memory factor (f) that is a fraction indicating the weight placed on past information; 1-f is the weight placed on the most recent LPUE. If the fraction is 0.5, then the memory retained is the average of the previously stored and just obtained LPUEs. If the fraction is 1, then the old information is retained and the new information is ignored. If the fraction is 0, then the old information is forgotten. Of the captain’s characteristics, only the captain’s memory, but not the memory factor, varies over time during the simulation.
Observations and interviews determined that captains routinely keep detailed logs of their fishing activities, both handwritten and in electronic format, so that an extensive history of the fishing experience is routinely available to most captains in the fleet. The value of this information can be expected to degrade over time as fishing, recruitment, and natural mortality impact the distribution and abundance of the stock. Certain captains rely more heavily on a longer term integration of their fishing experiences than do others. For simulations discussed here, captains were assigned memory weights of 0.2 and 0.8 or 0.98 and 0.99 (Fig. 3). Thus, certain captains’ memories were biased towards new or old information, respectively. Responsive captains, given a memory weight of 0.2 or 0.8, based fishing decisions on performance within the previous 1 to 6 weeks depending on the value of f and the number of trips taken per week. Obdurate captains, given a memory weight of 0.98 or 0.99, based fishing decisions on performance over a much longer period of time (7 months to well over 1 year). The responsive captain is considered an average captain in today’s fleet and is used subsequently as a point of comparison to captains exercising alternative behaviors.
Captain’s Idiosyncrasies
The captain is conferred certain degrees of boldness, inquisitiveness, skill, and loquacity (Table 2).
Skill, ranging between 1 and 10, determines how efficiently the captain conducts the fishing venture; that is, skill determines the fraction of time on the fishing ground during which the dredge is actively fishing. For these simulations, a captain with low skill fishes for 75% of the time while on the fishing ground whereas a captain with high skill fishes 100% of the time.
Boldness determines if the captain’s behavior includes searching behavior. In the current model, a timid captain never searches, a bold captain searches every time he leaves port, while the confident captain searches about 20% of the time, about once a month. In the surfclam fishery, vessels are expected to return to the dock within 48 hr during the warm months of the year. Thus, captains have limited time to search. Accordingly, in the model, when searching, the captain targets a random square within a 6-hr steam of the homeport regardless of his memory of past LPUE performance in that cell. Thus the bold captain, in effect, fishes randomly among a selection of 10-minute squares irrespective of the catch and a confident captain does so also, but 80% less often.
Inquisitiveness indicates whether or not a captain uses the most recent survey results to update his knowledge of the expected LPUE for each 10-minute square. Indifferent captains do not use the survey results, whereas inquisitive captains use the most recent survey. The federal survey frequency for surfclams is once every 3 years (NEFSC, 2013) and the provision of survey data to the public in the form of fishermen’s reports (e.g., NEFSC, 1999, 2002) occurs within a few months of the survey. These reports provide the raw tow results for each station on the survey. Thus, in these simulations, the inquisitive captain updates his memory every third year based on survey results.
Loquacity determines the tendency for a captain to share the results of his most recent trip with other captains. This propensity is invoked in the model in probabilistic terms. For these simulations, captains are either taciturn, so that information is never shared, or loquacious, so that the captain shares information to each other captain with a probability of 0.5.
Simulations were run with captains varying by only one trait relative to the standard, responsive captain. Thus, the responsive captain is responsive, skilled, timid, indifferent, and taciturn (Table 2). In contrast, the confident captain varies from this suite of traits in only one way, he is confident rather than timid; in other words, he searches occasionally. However in all other traits, he is identical in behavior to the responsive captain (Table 2). Similarly, the loquacious captain is identical to the responsive captain in all but one trait; he is loquacious rather than taciturn.
Processing Plant
The two major functions of the processing plants are to buy clams from the boats and to set the weekly quota for the fleet of boats fishing for the plant. Surfclam fishing vessels are strictly tied to plants, so that no vessels fish for more than one plant. The weekly quota controls the number of fishing trips per week. The surfclam fishery is an ITQ fishery. For the purposes of this study all plants are assumed to own an equivalent number of ITQ shares and to have fleets with equivalent fishing powers. Consequently, the quota is distributed evenly as a consequence of the even distribution of ITQ shares.
The harvest quota for the year is calculated at the time of the November survey of the previous year. On the first of January, this quota is distributed among the processing plants in proportion to the fraction of the total fishing power that is represented by the fleet that is attached to that plant. Each plant distributes its fraction of the total quota to its fishing boats in proportion to their hold size on a weekly basis. The weekly quota for a boat is limited to twice its hold size in order to limit fishing trips to no more than twice a week. This is consistent with the standard operating procedure in the surfclam industry. As much as possible, the weekly quota is distributed to boats in allocations equivalent to full hold capacity.
If the weekly quota for a boat averaged over the year is below twice its hold size, then the boat cannot complete two trips per week over the entire year. In this case, the quota is shifted in the year so that the largest quota occurs in the months when meat yield is the highest. In the present model, the 20th week of the year has the largest yield. During this time, boats can take two trips per week to the extent that the number of total trips exceeds one trip per week each week of the year. Consequently, one-trip weeks are allocated to periods when yield is low. This maximizes the profit for the plants. The weekly quota is renewed at the beginning of the week, defined to be Sunday in the model.
The plants pay the boats $12 (surfclam bu)-1 for the landed surfclams. For the purposes of these simulations, all other plant economics are inconsequential to the outcome of the analysis and thus are not reported in this study.
Weather
Fishing may cease due to weather, primarily in the winter. Thus, weather was imposed as a factor for 6 months of the year (October–March). The frequency of different winter wind speeds was obtained from two NOAA meteorological buoys (NDBC 44008 over Nantucket Shoals and NDBC 44009 off Cape May). This wind analysis gave the fraction of time that boats of different sizes could fish. For the simulations here, weather of intensity 5, 4, 3, 2, 1, 0 occurs 5%, 10%, 15%, 20%, 30%, and 20% of the time, respectively. The higher weather index indicates higher winds.
Boats of increasing size have increasing boat indices that range from 1 to 4. The weather effect is imposed by restricting boats with an index less than the weather code from leaving port. In the model, during winter, the weather code for the current day is determined by a random draw and this determines which boats can fish. Boats already at sea are not affected by the current weather. Most fishing trips are at most two days long so this weather restriction on leaving port is effective without requiring, in the model, that boats at sea return to port in bad weather. For this study, small boats were given a weather code of 1 and large boats a weather code of 3. Thus, small boats have a 50% chance
on any given day of leaving port in the winter; large boats have an 85% chance.
Surfclam Biology
Initial clam distribution
The initial surfclam distribution (clams m-2 per size class) is calculated in two steps. A biomass for the total population is imposed as an initial condition for the simulation. This biomass is distributed among 10-minute squares as a total clam density (summed over sizes) using a negative binomial random distribution to create a patchy distribution over the 10-minute squares in which surfclams can exist. Then, a spatially-varying size distribution is used to distribute the surfclams in each 10-minute square into size categories. Patchiness is maintained subsequently by recruitment, as described in a later section.
The growth and mortality rates for the surfclam population are specified separately for different simulations so the originally specified population size-frequency and density distribution may be inconsistent with these parameters. The model initial conditions are adjusted by running the model for 100 years without fishing to allow the initial population to adjust to the chosen rates of growth, mortality, and reproduction. Fishing in each model run, therefore, begins with a virgin stock.
Size and growth
The clams are distributed in 18 length classes of 1-cm interval starting at 2 cm and extending to 20 cm. The average length for a size category is the average of the lengths on either edge of the box. So, for example, the first size category includes all clams between 2 and 3 cm in length and has an average length of 2.5 cm.
The average wet weight for the animals in each size category is calculated with an allometric relationship of the form
 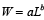 . (1) . (1)
Parameter values come from Marzec et al. (2010).
A daily growth rate for each size class for each 10-minute square was calculated from the von Bertalanffy age-length relationship for that square:
 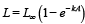 (2) (2)
where L is length in mm and A is age in years. L∞ is the largest length for the clam and k (yr-1) is the rate that the smallest clams grow. The von-Bertalanffy parameters were estimated from information provided by the federal surfclam survey (NEFSC, 2013; see also Munroe et al., 2013). The growth rate (length change per time) is determined for each size class by calculating the age of the clam at the smaller edge of the length box. Then the length of the clam one year younger is calculated from the von Bertalanffy relationship. The one year length change divided by the length change over the length of the box determines how quickly clams move from one box to the next.
Natural mortality is imposed once yearly using a specified instantaneous mortality rate m that is the same across all size classes. Munroe et al. (2013) raise the issue of increased mortality at old age, consistent with other bivalves (see Powell et al., 2012). However, the presently-accepted stock assessment model retains the constant mortality assumption consistent with Weinberg (1999). The present model follows the assessment approach.
Growth and mortality vary by 10-minute square. This is accomplished by specifying the values of k, L∞, and m at the corners of the domain and assigning values to each 10-minute square by interpolation. In cases where a more complicated cross-shelf distribution is desired, values at the mid-points of the domain are also specified prior to interpolation. This permits latitudinal and cross-shelf variations in growth and mortality (Weinberg, 1999; Chintala and Grassle, 2001; Weinberg et al., 2002; Munroe et al., 2013).
For the 1990s simulations, the mortality rate is isotropic and specified as 0.15 yr-1. For the 2000s simulations, mortality rate increases from this rate southeasterly across the domain to reduce surfclam abundance at the southern and inshore extremes of the range, consistent with Weinberg (1999, 2005). The von-Bertalanffy parameterization results in higher growth rates, with k~0.26 yr-1 in the 1990s, but relatively isotropic over the range. The 2000s values vary latitudinally from 0.25 yr-1 in the south to 0.19 yr-1 in the north and decline offshore to 0.15 yr-1. L∞ varies latitudinally in both time periods with values from 150 to 164 cm in the 2000s and somewhat higher in the 1990s.
Reproduction
Surfclams recruit to the population one day per year, chosen arbitrarily to be October 1. The total number of recruits is calculated from the total population biomass. A stock-recruit relationship is not available for surfclams. Beverton-Holt parameters are estimated for the virgin stock from an input value for steepness, set at 0.8 for these simulations, following the method of Myers et al. (1999; see also O’Leary et al., 2011). Each year, total recruitment is calculated using the Beverton-Holt relationship and the total stock biomass. Interannual variability is imposed by obtaining a random factor that is applied to the total number of recruits. Recruitment is parsed out to each 10-minute square by adding individuals to the smallest size class (20 mm) based on a negative binomial distribution which makes the cell-wise recruit process patchy. The smallest size class used is consistent with juvenile growth rates that show that newly settled surfclams can reach 20 mm by the end of the settlement year (Chintala and Grassle, 1995; Ma et al., 2006).
Meat yield
Meat yield for a surfclam depends on the time of year and the 10-minute square. Yield is measured as usable meat and is about 75% of the wet meat weight. As part of model setup, a yearly minimum and maximum yield is specified for an average market-size clam. The actual yield for a given fishing trip depends on the time of year since clam meats are heavier in late spring through early fall during the spawning season (Ropes, 1968; Jones, 1981; Spruck et al., 1995). A 5th-order polynomial based on the day of the year provides a time-varying yield between 11 and 15 lb (surfclam bu)-1. This yield curve was obtained from the industry who retain detailed records of yield as part of their economic planning. The meat weight for the clams of different sizes is determined from the allometric relation (equation 1). The weight of clam meat in a bushel is calculated from the number of clams of a given size in a bushel and the wet weight of the clams of that size, standardized to the yield curve using the weight and yield of a 150-mm clam.
Choosing a Fishing Location
A captain chooses a fishing location by the following rational processes based on his memory log. For those captains not searching, the captain calculates the time to steam from the port to each 10-minute square in turn. Then the captain calculates how many hours would be required to fill his boat based on his remembered LPUE. The captain chooses to fish in the square for which the fill time is least and the distance to the square shortest in order to minimize time at sea while returning to the dock with a full load. Interviews with industry representatives emphasize the time-at-sea criterion. The captain is assumed to know LPUE in whole cage units per hour. Thus, a number of 10-minute squares may have the same LPUE. Accordingly, the captain identifies one or more 10-minute squares that maximize LPUE and chooses among these for his next trip the 10-minute square nearest to port.
Fishing Details
The number of surfclams harvested during an hour of fishing is calculated from the area swept by the dredge, which depends on the tow speed and dredge width, the efficiency of the dredge, the size selectivity of the dredge, and the skill of the captain. In addition, the harvest is reduced if the harvest rate per hour exceeds the boat’s handling capacity. The number of hours fished is determined by the time necessary to fill the vessel, as constrained by the allowed time on site given the steaming time to return to port. Vessel characteristics were obtained from vessel captains and industry representatives. Selectivity and efficiency relationships were obtained from the federal survey program (e.g., NEFSC, 2013; see Rago et al., 2006 and Hennen et al. 2012 for additional details).
At the beginning of the fishing hour, if the total catch for the trip has reached the boat capacity or if the available time-at-sea has elapsed, then fishing stops and the boat returns to port (Table 1). Boat capacity is defined in terms of cages, a volumetric measure, whereas individual clams of varying sizes are caught by the dredge. Numbers are converted to volume based on the number of clams of various size classes per bushel. The number of clams per bushel for a given 1-cm size interval was obtained from direct counts of clams of known size landed in Atlantic City, NJ in 2012. Thus, each sized clam is associated with a volume occupied in the bushel, including clam plus void space, and the volumes summed to estimate the total cage volume provided by the dredge haul.
Survey Details and the Annual Quota
A complete survey of the surfclam population is conducted on November 1. This allows the survey to record the most recent recruitment event. The survey is perfect in that it uses the true clam density for each 10-minute square and samples every square. The survey determines the biomass of the fishable stock, specified for these simulations as all clams ≥12 cm. This size is consistent with industry dredge selectivity curves that show high catch efficiency for clams ≥12 cm (NEFSC, 2013). The stock survey uses a survey dredge that can be different from that used by the fishing boats in its efficiency and size selectivity. Up through the latest (2012) federal survey (NEFSC, 2013), that difference was significant in that selectivity of the survey dredge was dome shaped and smaller clams were caught more efficiently than with the industry dredge (NEFSC, 2013).
The total fishable biomass (Fbio) is used to set the annual quota based on two reference points, biomass at maximum sustainable yield (Bmsy) and the fishing mortality rate, Fmsy, yielding msy at Bmsy. Fmsy was set to 0.15 yr-1 (NEFSC, 2013). Bmsy was set to half of the carrying capacity established by the biomass of the virgin stock after 100 years without fishing. The ABC biomass (ABCbio = allowable biological catch), which is the allowed annual fishing quota for the next year, is calculated using the following rules:
 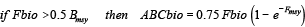 ; (3) ; (3)
 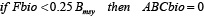 ; (4) ; (4)
 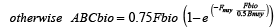 . (5) . (5)
The annual quota biomass is converted to bushels of clams and is capped by an imposed total allowable catch, which in these simulations is 3.5 million bushels. This cap is established by the fishery management plan (FMP) (MAFMC, 1986).
Simulations
Simulations were performed to compare a series of behavioral choices available to the captains, identified through interviews with industry representatives and captains. These choices include (a) the degree to which captains rely on recent catch history to determine where to fish, (b) whether a captain undertakes searching behavior to determine where to fish, (c) the degree to which captains communicate with each other about their catches, (d) the skill of the captain while fishing, and (e) the degree to which captains avail themselves of federal survey data. Although illegal harvesting is often a component of behavioral choice (e.g., McCay, 1984; Haring and Maguire, 2008; Bashore et al., 2012), the requirement that each cage of surfclams receive a tag prior to off-loading has eliminated illegal fishing from the surfclam industry; thus illegal harvesting was not included in this study as an option.
We compared two vessel sizes, small and large, and four ports that encompass most of the primary homeports as they have existed over much of the history of the industry. We included two domains, one typical of the 1980s-mid-1990s prior to the most recent phase of warming of the Mid-Atlantic Bight, wherein surfclams extended in plentitude to the Chesapeake Bay mouth, and one typical of the 2000s, post-warming, wherein the surfclam range was compressed northward as a consequence of the demise of surfclams inshore from the Delmarva Peninsula to north of Delaware Bay (Fig. 2). During this time, the southernmost ports used in the simulations became uneconomic and thus we include in the post-warming domain ports that are no longer functioning for the surfclam fishery.
We ran 51-year simulations and used the last 25 years to remove the effect of initialization of the captain’s memory log in year 1 and to permit the stock to be fished down below virgin stock size. Analysis of simulation results focused on the following metrics: the time spent fishing, the differential in catch between that anticipated if all trips returned to port fully loaded and the landed catch, the distance traveled by the boat to the fishing ground, LPUE (calculated as  ), the number of 10-minute squares fished per year, and the net revenue for the vessel. Net revenue is calculated relative to a stipulated ex-vessel value of the catch and the cost of fuel; accordingly, relative variations in net revenue are more important than the actual value. We did not vary the biological processes determining stock performance and distribution during a simulation. Stock biomass was set to approximate the density of clams observed by the federal survey (NEFSC, 2013). As a consequence, the biological reference points did not affect the outcome as the ABC always exceeded the FMP cap. Thus, the quota was invariant over the 51-simulated years. This is precisely the case for the surfclam fishery for most of the 2000s (NEFSC, 2013). ), the number of 10-minute squares fished per year, and the net revenue for the vessel. Net revenue is calculated relative to a stipulated ex-vessel value of the catch and the cost of fuel; accordingly, relative variations in net revenue are more important than the actual value. We did not vary the biological processes determining stock performance and distribution during a simulation. Stock biomass was set to approximate the density of clams observed by the federal survey (NEFSC, 2013). As a consequence, the biological reference points did not affect the outcome as the ABC always exceeded the FMP cap. Thus, the quota was invariant over the 51-simulated years. This is precisely the case for the surfclam fishery for most of the 2000s (NEFSC, 2013).
Results
Certain outcomes of the model depend on the choice of random numbers, particularly the distribution of recruits among 10-minute squares. Consequently, a series of simulations was conducted to evaluate the influence of random number on simulation outcome (Fig. 4). This analysis showed that the choice of seed number for the random number generator did not substantively affect the economics of the vessel, LPUE, hours spent fishing, average distance traveled from the port to the fishing ground, or the degree to which the vessel returned to port fully loaded. Thus, results presented subsequently are limited to single simulations for each combination of decade (1990s versus 2000s), vessel size (small versus large), and captain’s behavioral choice.
The yearly quota is ultimately distributed to each boat in proportion to its hold capacity. Vessels can take up to two trips per week, but the available quota does not permit two trips per week for each week of the year. Poor fishing performance limits the success of trips and this is measured by the differential between the catch landed and that which could be landed if the boat arrived at the dock full. Simulations showed that small boats normally caught most of their yearly quota allocation (Fig. 5). Large boats performed distinctly more poorly. Boats fishing out of Port 1, the southernmost port, failed to catch their quota allocation to a much greater extent than boats fishing out of the other 3 ports (Fig. 5). That is, vessels fishing out of Port 1 often returned to the dock only partially full. With rare exceptions, vessels fishing at consecutively more northerly ports showed improved performance relative to the neighboring port to the south. Both of these outcomes are anticipated by the contraction of the surfclam’s range at its southern and inshore boundaries that increases the time steaming to the more distant fishing grounds in the south and thus reduces the time spent fishing during the trip.
The behavioral choices available to the captains introduced clear differences in performance (Fig. 6). Simulations showed that captains that searched frequently (bold captains) performed less well than the standard (timid) captains with the exception of skippers of large vessels from Port 1 where bold captains performed better. Captains that fished with lesser skill performed poorly relative to the standard (skilled) captain. Those that used a longer period of past performance (obdurate captains) to choose fishing locations and those that communicated (loquacious captains) tended to perform less well than captains that used survey data (inquisitive captains) or occasionally searched (confident captains), but this trend was primarily a feature of large vessels fishing from northern ports (Fig. 6).
More of the allocated quota was caught under 1990s compared to 2000s conditions for nearly all vessel-port combinations (Fig. 7). Simulations indicated that differences were greatest at southern ports where vessels underperformed to a much larger degree under present-day conditions in comparison to the past. Captains that searched and responsive captains, those that made fishing decisions based on the most recent catch record, were most penalized if fishing out of Ports 1 or 2. Captains of large vessels that based fishing decisions on a longer term remembrance of past performance were also penalized if fishing from Ports 1 or 2. Overall, however, the behavior of captains little influenced the degree of difference between past and present-day performance. Changes in the distribution of the stock relative to the vessels’ homeports and vessel characteristics dominated the outcome.
Simulations showed that large vessels were more profitable than small vessels under present-day conditions (Fig. 8). Simulations of small vessels often indicated that these vessels were not being operated at a profit. This is consistent with interviews of participants in the industry that reported that vessel operations were frequently subsidized in some measure by the processing plants for which they fish. Nevertheless, economic information for these vessels is sufficiently uncertain in terms of fuel prices, clam prices, and maintenance costs that the following economic analyses focus on the differential in revenue between simulated cases rather than the absolute values.
Simulated vessels fishing from more northerly ports were more profitable than those with southern homeports. Profitability increased modestly if captains communicated (loquacious), used survey data (inquisitive), or occasionally searched (confident) (Fig. 9). Profitability decreased with low skill and with frequent searching (bold captains). Profitability was higher for all boat-port combinations under past conditions. Stock contraction was the dominant arbiter in the comparison of net revenues between past and present day. Greatest changes occurred for vessels fishing out of Port 1 and a south to north trend was frequently present, such that the differential between past and present day was less at more northerly ports, consistent with the greatest changes in stock distribution being farther south. The behavior of captains did not noticeably affect the outcome.
Simulated LPUE averaged about 1.5 to 2 cages per hour on small boats except for Port 1 where values nearer one were obtained regardless of captain under present-day conditions (Fig. 10). Simulated LPUE on large boats averaged around 3 to 4 cages per hour regardless of port, again with the exception of Port 1 (Fig. 10). Captains with low skill and obdurate captains, those using a longer record of performance to choose a fishing location, underperformed, as did loquacious and bold captains, particularly those fishing from more northerly ports (Fig. 11). Use of survey data improved performance modestly for captains fishing out of Port 1 (Fig. 11). Occasional searching (confident captain) offered little benefit. LPUE did not vary consistently between past conditions relative to present day (Fig. 12). LPUE for large vessels tended to be higher under present-day conditions at more northerly ports. LPUE for captains that searched declined in the 2000s in most cases, whereas the outcome for other behavioral choices was port and vessel specific without consistent trend.
Simulations under present-day conditions showed that large boats fished farther from their homeport on the average (Fig. 13). Thus, total distance traveled per year averaged higher for large vessels than small vessels. This is consistent with the higher steaming speed for large vessels. Vessels fishing out of Port 1 traveled much farther than vessels fishing out of other ports. Often, but not always, vessels fishing from the two most northerly ports traveled a lesser distance than vessels fishing from Port 2. The distance traveled decreased if captains communicated or used survey data, but only if fishing from the three more northerly ports (Fig. 14). Behavioral choice little influenced distance traveled when fishing out of Port 1, except if the captains of large vessels searched. Searching reduced travel time from Port 2, but increased travel time in most cases. Reduced distance traveled did not necessarily improve vessel economics. For example, distance traveled declined for the loquacious captain, but so did LPUE, so that net revenue was only modestly affected. The distance between port and fishing ground increased under present-day conditions compared to the past for most port-vessel combinations. Largest differences were at Port 1; smallest at Ports 3 or 4. Searchers (confident and bold captains) were least affected overall, as these captains tended to steam farther from port regardless of stock distribution (Fig. 15). Captains with low skill or who based fishing decisions solely on catch history (responsive and obdurate captains) were impacted more than loquacious captains or captains that used survey data (inquisitive captains). Thus, responsive captains, those who based fishing decisions on recent catch history, tended to travel less far from port in the past than present day relative to captains that searched. Captains that used the survey or that communicated tended to travel less far from port in the past than present day relative to responsive captains (compare Figs. 14 and 16).
Large vessels spent more time fishing than small vessels, consistent with their larger hold capacity, the differential effect on vessel economics being mitigated by their higher LPUE. Differential in time at sea was primarily a function of the choice of fishing location, not time spent fishing. Effort typically increased to the south with vessels from Port 1 exerting substantially more effort than vessels from other ports (Fig. 17); this consequently lowered LPUE (Fig. 10). The behavior of captains influenced effort. For captains of low skill, captains that employed a longer-term remembrance of past fishing activities in determining locations to fish (obdurate captains), and bold captains, those that frequently searched, effort increased relative to the standard (responsive, skilled, timid) captain (Fig. 18) at most ports. The singular exception was the influence of behavior for large vessels fishing out of Port 1. Here, effort decreased relative to the standard captain for loquacious captains, captains that used survey data (inquisitive), and captains that searched. These vessels traded increased steaming time to fish where LPUE was higher, thereby reducing fishing effort. Hours fished increased in some cases and decreased in others under present-day conditions in comparison to the past (Fig. 19). This conforms with the highly port-specific and vessel-specific effects on LPUE imposed by a contraction in the surfclam’s range. The differential tended to be greatest for Port 1 where effort was higher in the past due to the much greater time spent steaming under present-day conditions. Effort increased with frequent searching under present-day conditions, but LPUE was higher in the past, which explains the increased tendency for vessels fishing out of Port 1 to return to port without a full load under present-day conditions. Thus, frequent searching from southern ports was less beneficial as range contraction occurred.
Simulations under present-day conditions showed that most vessels fished on fewer than 10 10-minute squares per year regardless of vessel size or port (Fig. 20). Bold and confident captains visited significantly more 10-minute squares, consistent with their searching behavior. Bold captains visited more 10-minute squares than confident captains in keeping with their higher searching frequency, but not proportionately, as just so many squares could be reached by these vessels in the allotted time at sea. Thus bold captains often revisited 10-minute squares, whereas confident captains did not. The effect was most pronounced for small vessels that were more limited in their searchable region due to their slower steaming speeds. Captains that used survey data (inquisitive captains) also visited an increased number of 10-minute squares. Fewer 10-minute squares were visited by vessels fishing from Port 1. The number of 10-minute squares fished in a given year changed little in the present day relative to the past; however, decreases occurred for captains that searched from southern homeports, Ports 1 and 2 (Fig. 21). This is consistent with the fewer 10-minute squares available to the fishery during present-day conditions for vessels sailing from southern ports.
Discussion
Perspective
Surfclams are relatively long-lived relatively immobile animals (Alexander et al., 1993; Weinberg, 1999). Their distribution is dramatically patchy on the scale of 10-minute squares (e.g., Weinberg et al., 2005). These two characteristics generate the most noticeable pattern in the spatial and temporal distribution of effort in the fishery. Vessels tend to return routinely to the same few 10-minute squares and thus a small area of the stock’s range supports the majority of the fishery (e.g., NEFSC, 2013; see e.g., Mahévas et al., 2008 for another example of repeated fishing in constricted locations). Because the quota is set well below the allowable biological catch (ABC) by the fishery management plan, the fishery imposes a low fishing mortality rate on the stock; ergo, variations in fishing performance occur slowly because 10-minute squares are fished down over a relatively long period of time. The model reproduces this behavior precisely based on a biological stipulation that the clam is patchy on the scale of 10-minute squares and the premise that captains choose locations to fish that minimize time at sea while permitting the landing of a full vessel load. Thus, determination of the fishing ground for the next trip is based on known catch history and steaming time from port. Here, we examine the influence of a change in stock distribution and a range of behavioral modifications available to the captains that might modify this standard operating procedure.
Given a vessel of average age and thus maintenance cost, a pre-determined ex-vessel value for a bushel of clams, and assuming unbiased availability of quota across the fleet, a vessel’s economic performance is primarily determined by time at sea. As fuel use increases while fishing and as fishing consumes a significant portion of time at sea, minimizing fishing time is as important as minimizing steaming time. Setting aside the seasonal and geographic differences in yield (Loesch and Evans, 1994; Marzec et al., 2010; Munroe et al., 2013), the fleet performance for vessels sailing from a single port is dominated by the degree to which the quota allocated to that port is caught by the vessels fishing therefrom and the degree to which the net revenue for a vessel must be supported by the plant to maintain a positive cash-flow balance. The surfclam industry is vertically integrated, so that plant and vessel profitability are to a certain extent fungible.
Thus, a number of measures of profitability are investigated here, including the degree to which the weekly quota expected to be landed by the vessel was caught and the net revenue for the vessel, a number of measures of vessel performance, including LPUE and fishing effort, and other aspects of fishing behavior, including the number of 10-minute squares visited yearly and the distance from port to the fishing ground. We examined two time periods, a period prior to the late 1990s when the stock south of Long Island was distributed over a broad area of the inner continental shelf from northern New Jersey to Chesapeake Bay and the present-day distribution which includes the expansion of the population inshore along Long Island and a large recession of the southern stock boundary off Delmarva (Weinberg, 2005; Kim and Powell, 2004). The manifest impact of this shift in distribution on the fishery is the decline of clam processing south of New Jersey, the cessation of fishing first from Port 1 (Norfolk, Virginia), and more recently Port 2 (Ocean City, Maryland), and a decline in landings resulting in an increase in uncaught quota (NEFSC, 2013).
The influence of stock distribution
The influence of stock contraction is evinced by a number of metrics in these simulations. In most cases, the differential between the 1990s domain and the 2000s domain occurred throughout the fishery but with a distinctly larger impact farther south. Net revenue declined as vessels steamed farther from port to go fishing and more frequently returned without a full load, although most vessels still returned over 80% full north of Port 1. The differential was dramatically larger for Port 1, the southernmost port, and routinely larger for Port 2 than for Ports 3 and 4. In a few cases, the differential for Port 3 (Atlantic City, New Jersey) was least. Port 3 rests at the latitudinal center of the surfclam’s range in the Mid-Atlantic Bight and so is least influenced by shifts at the stock boundaries. Overall, however, net revenue declined between the 1990s and the 2000s, particularly for the southern ports, while changes in LPUE were highly port and vessel specific with little overall pattern, the differential in net revenue being determined primarily by the tradeoff between time fishing and time steaming to 10-minute squares capable of supporting an adequate LPUE. Only the tendency for large vessels to return to port without a full load suggests that large vessels became less economically viable relative to small vessels as a result of stock contraction, but the effect was also restricted to Ports 1 and 2, the southernmost ports. Thus, the differential observed in these simulations was port specific and vessel size-specific.
In the model, large vessels retain a positive revenue stream except at Port 1, whereas small vessels are not profitable at any port. Part of this differential comes from the older age of the smaller vessels that results in higher fixed costs (see model description). Part is due to the lower LPUE. However, simulated small vessels catch their weekly quota allotment more consistently than large vessels and this is not reflected in the vessel net revenue calculation whereas it would be important in the economics of the processing plants: the economics of processing plants are not considered in this study. Thus, the model does not identify an overall bias in performance between the two vessel sizes, although it suggests that continued range contraction may disproportionately impact the larger vessels. Economic and performance data are not available to verify many of these conclusions, but the abandonment of Ports 1 and 2 over the last decade is a clear indicator of an overall decline in vessel performance from these ports. This decline is explained in the model by a relative decline in net revenue and an increase in total distance traveled at sea for vessels sailing from these two ports that results in these vessels more frequently failing to catch their weekly quota allotment.
Behavioral Choice by Captains
Simulated vessel performance agreed with observations using a few simple rules that relied mostly on recent catch history and the need to limit time at sea. Variations in the behavior of captains under present-day conditions did not much modify the outcome overall. That is, trends in vessel performance based on vessel size and location of homeport were little influenced overall by a range of behavioral modifications diverging from these simple rules.
Reducing skill, thereby increasing effort, reducing LPUE, reducing profitability, and increasing uncaught weekly quota serves to contrast an underperforming captain relative to the responsive captain that fishes according to two simple rules: Rule 1, captains choose locations to fish that minimize time at sea while permitting the landing of a full vessel load; and Rule 2, the information that is used by Rule 1 to determine fishing location is based on the most recent catch history for the vessel. This typical captain is defined as a skilled captain that identifies fishing locations based upon recent catch history (responsive), rarely communicates (taciturn), does not search (timid), and does not use survey data (indifferent). In these simulations, the low-skill captain was specifically defined to perform poorly in comparison to this typical captain.
Some captains may use a longer-term catch history. Obduracy would seem an inappropriate behavior as surfclam densities are unlikely to increase significantly within a previously fished 10-minute square on time periods of one-to-two years and any catch history older than several years is unlikely to provide accurate information as surfclams can grow to market size within 3–4 years (e.g., Munroe et al., 2013). Captains no doubt remember locations where submarket clams have been seen and may return to those 10-minute squares some years hence. This behavior was not modeled in this analysis. Here obduracy degrades performance when it affects performance at all. Large vessels fail to meet their weekly quota obligations more often, for example, when skippered by obdurate captains (Fig. 6). LPUE is modestly lower for both vessel sizes (Fig. 11). Simulations reinforce the value of returning repeatedly to a few 10-minute squares, a behavior that can be inferred to be advantageous from the known record of fishery landings (NEFSC, 2013). Simulations also reinforce the need for captains to obtain information on fishing locations independent of their personal experience.
Captains report a limited degree of communication within the fleet concerning recent catch histories. In these simulations, loquacity modestly improved performance, particularly by reducing distance traveled (Fig. 14), but the effect was sufficiently limited to suggest that the value of communication will not overbalance the natural tendency for captains to compete in performance. Profitability was marginally affected (Fig. 9) giving limited rationale to modify the competitive nature of between-vessel interactions. Thus, model and observation agree that communication between captains normally is not sufficiently valuable in improving fishing performance to counterweigh the propensity of captains to keep their fishing strategies secret. These results for a fishery on sessile molluscs contrast to a finfish fishery described by Holland and Sutinen (2000) where communication was important due to the mobility of the species.
Searching occurs in most fisheries; however, the success of searching behavior is highly variable (e.g., Dorn, 2001; Powell et al., 2003a,b; Millischer and Gascuel, 2006; Bertrand et al., 2007). Surfclam captains report limited searching behavior, though they also report a desire to search more frequently than vessel owners permit. Simulations provide an explanation for this dichotomy. Simulated bold captains, those captains that search frequently, visit many more 10-minute squares than captains with any other behavior (Fig. 20). However, these captains routinely underperform as measured by a variety of metrics. Less of the weekly quota allotment is landed (Fig. 6) and distance traveled from port to fishing ground increases (Fig. 14). LPUE declines (Fig. 11), as does profitability (Fig. 9). Most 10-minute squares produce less than locations known to support high LPUE, so targeting a random 10-minute square on a given fishing trip is very much more likely to reduce performance on that trip than to increase it. Moreover, the bold captain is likely to return to a subpar 10-minute square more than once. Powell et al. (2003a,b) and Gillis et al. (1993) report other instances where searching lowers LPUE. In contrast, the confident captain searches occasionally. This captain fishes in an increased number of 10-minute squares yearly, but fewer than the bold captain, and rarely returns to an unprofitable square. This captain has modestly increased profitability (Fig. 9) because he remembers and thus returns to the occasionally-found 10-minute square that supports improved LPUE and lesser time at sea. The dichotomy between captains desiring to search and owners limiting requital would appear to stem from an inability to discern the degree of searching leading to a beneficial result relative to its exceedance leading to a disadvantageous outcome.
The surfclam stock is surveyed approximately triennially (NEFSC, 2013). Cruise reports are released to the public soon thereafter (e.g., NEFSC, 1999, 2002). These reports may be valuable in that surfclams, unlike finfish, are immobile at the scale of a 10-minute square and their recruitment and mortality rates auger for considerable stability in market-size abundance over a few years time. Some captains are observed to use these survey reports. Simulations of inquisitive captains showed that survey use improved performance in a number of metrics. The survey reports are, in essence, a free and comprehensive search and the time scale is consistent with surfclam growth rates to market size. That is, one might expect surfclam densities to vary within 10-minute squares on a 3–5 year time span, relatively coherently with the triennial survey.
However, even the greatest differential, the comparison of an unskilled captain with an inquisitive one, shows a limited range in performance. That is, the repertoire of behavioral choices available to captains offers on the one hand only a limited range for improvement in performance, while invoking on the other hand only limited additional risk of deterioration in performance. This outcome is preordained by the sessility of the surfclam and its long life span and low natural mortality rate that foster long-term stability of patches at the 10-minute-square scale of the fishery. Thus, captains need not be imbued with extraordinary sagacity to come close to optimal fishing results, as the implementation of two simple rules, that captains choose locations to fish that minimize time at sea while permitting the landing of a full vessel load and that the information that is used to determine fishing location is based on the most recent catch history for the vessel, are sufficient to achieve near optimal performance.
Impetus for behavioral adaptation
Presumably, whatever positive effect behavioral choices may imbue offers increased advantage during times of stock range contraction which reduces the inherent viability of certain homeports and vessel sizes. In fact modeled behavioral choices little influenced the performance metrics between past and present day. Although the fraction of quota uncaught increased from the past to the present day in these simulations, the change was little modulated by the repertoire of options available to the captains (Fig. 7). Variations in behavior varied the average distance traveled from port to fishing ground more in the past (Figs. 14 and 16) probably because a wider range of fishing locations were available prior to range contraction. Captains with low skill performed more poorly under present-day conditions; however, no other behaviors disproportionately impacted performance relative to the standard (responsive) captain under present-day as compared to past conditions, either beneficially or disadvantageously. This study did not investigate cases where surfclam abundance fell sufficiently to force the annual quota below the FMP cap, however, this happenstance has not occurred over the time span of the ITQ fishery (NEFSC, 2013). Thus, certain behaviors may provide increased advantage or disadvantage at lower stock abundances than have been typical over the multidecadal history of the fishery.
Model Structure
Fishing vessels are operated by captains that routinely make choices concerning locations to fish. These choices are constrained by vessel characteristics and demands imposed by vessel owners and shore-based dealers. Their aggregate determines performance and performance can vary substantially from vessel to vessel and captain to captain (Dorn, 1998; Gillis et al., 1995b; Holland and Sutinen, 2000; Powell et al., 2003a,b; Monroy et al., 2010). The behavior of a fishing fleet and its performance variability has received considerable attention. Models have been constructed in a variety of ways, with individual-based information being implemented in varying degrees (e.g., Bockstael and Opaluch, 1983; Béné, 1996; Holland and Sutinen, 2000; Dorn, 2991; Hutton et al., 2004; Mahévas and Pelletier, 2004). In actuality, however, observed dynamics are the sum of trip-wise choices of location and trip-dependent differences in performance and the degree to which longer-term variability in stock dynamics might influence such outcomes may be difficult to extract from models that aggregate information or responses. Here, we have utilized a model that specifies independently each vessel and imbues each captain with specific behavioral proclivities. The model permits captains to respond daily to time-dependent phenomena such as quota allocation and weather. As a consequence, each vessel operates in an inherently independent way and fleet performance is the sum of a set of independent outcomes. As a consequence, this model attempts to reproduce as closely as possible the individual-based dynamics of a fishing fleet. The model reproduces observed dynamics reported in the literature (e.g., NEFSC, 2003, 2013) and in interview with surfclam captains and industry representatives (see also McCay et al., 2011) and permits investigation of the important components of behavior, vessel characteristic, and surfclam stock dynamic that generate the fleet-wide outcomes obvious in the time series of landings (NEFSC, 2013).
Conclusions
The response of the surfclam to warming of the Mid-Atlantic Bight is manifested in a substantial contraction of the range generated by the recession of the southern and inshore boundary. This phenomenon has impacted the fishery through the closure of southern ports and the movement of processing capacity north. Potentially, the challenges faced by the fishery require different responses on the part of the vessel captains to mitigate a decline in performance ineluctably accompanying this shift in range. The purpose of this study was to evaluate options in the captain’s repertoire that might mitigate the expected decline in performance.
A number of simulated behaviors modestly varied performance. Use of survey data and occasional searching tended to increase performance. Reliance on an older catch history tended to reduce performance as did frequent searching. However, in no case was this differential large and the differential was little modified by a contraction in the surfclam’s range. The population dynamics of the clam permit near-optimal performance based on a few simple rules: choose locations to fish that minimize time at sea while permitting the landing of a full vessel load; base this choice on the most recent catch history for the vessel.
A model based on this behavior and the appropriate abundance and patchiness of clams reproduced observed spatial and temporal trends. These included the south-to-north gradient in performance consistent with increased stock abundance north and the tendency for the fishery to repeatedly exploit a limited area of the stock’s range over the year (NEFSC, 2003, 2013). Comparison between the 1990s and 2000s demonstrated the increasing marginality of southern ports which is observed in the northward shift in vessel homeports and plant processing capacity. The frequency at which vessels failed to land their weekly quota allotment increased at southern ports and vessel profitability declined due to increased steaming distance to obtain a high LPUE. However, none of these changes compromised the basic approach to fishing observed in the industry and inculcated in the responsive captain used in this study because the underlying variables determining performance beyond port location are determined by the inherent sessility and patchiness of the clam and its long life span which result in temporal variations in patch location and density occurring slowly relative to the decision-making activities and trip frequency of the vessel captains. Accordingly, although captains can avail themselves of a range of approaches to obtain the information underpinning the choice of location for the next fishing trip, these differing approaches impart only modest competitive advantages or disadvantages to the final outcome.
Acknowledgments
Particular thanks to Dave Wallace, Jack Miles, Rob Jarmol, Joe Carch, Tom Hoff and a number of other industry representatives and captains that provided substantial information leading to the development and parameterization of SEFES. This study could not have been accomplished without their support. This project was funded by Award GEO-0909484 from the NSF Coupled Natural and Human Systems program. We appreciate this support.
References
ADELAJA, A., B. MCCAY, and J. MENZO. 1998. Market share, capacity utilization, resource conservation, and tradable quotas. Mar. Resour. Econ., 13: 115–134.
ALEXANDER, R. R., R. J., STANTON JR. and J. R. DODD. 1993. Influence of sediment grain size on the burrowing of bivalves: correlation with distribution and stratigraphic persistence of selected Neogene clams., Palaios, 8: 289–303. doi.org/10.2307/3515151
BASHORE, C. J., H. A. LANE, K. T. PAYNTER, M. NAYLOR, J. R. HARDING, and D. C. LOVE. 2012. Analysis of marine police citations and judicial decisions for illegal harvesting of eastern oysters (Crassostrea virginica, Gmelin 1791) in the Maryland portion of the Chesapeake Bay, United States, from 1954 to 2010. J. Shellfish Res., 31: 591–598. doi.org/10.2983/035.031.0301
BASTARDIE, F., M. VINTEHR, J. R. NIELSEN, C. ULRICH, and M. S. PAULSEN. 2012. Stock-based vs. fleet-based evaluation of the multi-annual management plan for the cod stocks in the Baltic Sea. Fish. Res., 101: 188–202. doi.org/10.1016/j.fishres.2009.10.009
BAUDRON, A., C. ULRICH, J. R. NIELSEN, and J. BOJE. 2010. Comparative evaluation of a mixed-fisheries effort-management system based on the Faroe Islands example. ICES J. Mar. Sci., 67: 1036–1050. doi.org/10.1093/icesjms/fsp284
BÉNÉ, C. 1996. Effects of market constraints, the remuneration system, and resource dynamics on the spatial distribution of fishing effort. Can. J. Fish. Aquat. Sci., 53: 563–571. doi.org/10.1139/f95-212
BERTRAND, S., A. BERTRAND, R. GUEVARA-CARRASCO, and F. GERLOTTO. 2007. Scale-invariant movements of fishermen: the same foraging strategy as natural predators. Ecol. Appl., 17: 331–337. http://dx.doi.org/10.1890/06-0303
BOCKSTAEL, N. E., and J. J. OPALUCH. 1983. Discrete modeling of supply response under uncertainty. The case of the fishery. J. Environ. Econ. Manage., 10: 125–137. doi.org/10.1016/0095-0696(83)90021-9
CHINTALA, M. M., and J. P. GRASSLE. 1995. Early gametogenesis and spawning in “juvenile” Atlantic surfclam, Spisula solidissima (Dillwyn, 1819). J. Shellfish Res., 14: 301–306.
CHINTALA, M. M., and J. P. GRASSLE. 2001. Comparison of recruitment frequency and growth of surfclams, Spisula solidissima (Dillwyn, 1817), in different inner-shelf habitats of New Jersey. J. Shellfish Res., 20: 1177–1186.
DORN, M. W. 1998. Fine-scale fishing strategies of factory trawlers in a midwater trawl fishery for Pacific hake (Merluccius productus). Can. J. Fish. Aquat. Sci., 55: 180–198. doi.org/10.1139/f97-234
2001. Fishing behavior of factory trawlers: a hierarchical model of information processing and decision-making. ICES J. Mar. Sci., 58: 238–252. doi.org/10.1006/jmsc.2000.1006
GILLIS, D. M., R. M. PETERMAN, and A. V. TYLER. 1993. Movement dynamics in a fishery: application of the ideal free distribution to spatial allocation of effort. Can. J. Fish. Aquat. Sci., 50: 323–333. doi.org/10.1139/f93-038
GILLIS, D. M., R. M. PETERMAN, and E. K. PIKITCH. 1995a. Implications of trip regulations for high-grading: a model of the behavior of fishermen. Can. J. Fish. Aquat. Sci., 52: 402–415.
1995b. Dynamic discarding decisions: foraging theory for high-grading in a trawl fishery. Behav. Ecol., 6: 146–154. http://dx.doi.org/10.1093/beheco/6.2.146
HARING, P., and J-J. MAGUIRE. 2008. The monkfish fishery and its management in the northeastern USA. ICES J. Mar. Sci., 65: 1370–1379. doi.org/10.1093/icesjms/fsn131
HENNEN, D., L. JACOBSON, and J. TANG. 2012. Accuracy of the Patch model used to estimate density and capture efficiency in depletion experiments for sessile invertebrates and fish. ICES J. Mar. Sci., 69: 240–249. doi.org/10.1093/icesjms/fsr212
HOLLAND, D. S., and J. G. SUTINEN. 2000. Location choice in New England trawl fisheries: old habits die hard. Land Econ., 76: 133–149. doi.org/10.2307/3147262
HUTTON, T., S. MARDLE, S. PASCOE, and R. A. CLARK. 2004. Modelling fishing location choice within mixed fisheries: English North Sea beam trawlers in 2000 and 2001. ICES J. Mar. Sci., 61: 1443–1352. doi.org/10.1016/j.icesjms.2004.08.016
JONES, D. S. 1981. Reproductive cycles of the Atlantic surfclam Spisula solidissima, and the ocean quahog Arctica islandica off New Jersey. J. Shellfish Res., 1: 23–32.
JOSSI, J. W., and R. L. BENWAY. 2003. Variability of temperature and salinity in the Middle Atlantic Bight and Gulf of Mexico based on data collected as part of the MARMAP Ships of Opportunity Program, 1978–2001. NOAA Tech. Mem. NMFS-NE-172, 92 p.
KIM, Y., and E. N. POWELL. 2004. Surfclam histopathology survey along the Delmarva mortality line. J. Shellfish Res., 23: 429–441.
LIPTON, D. W., and I. E. STRAND. 1992. Effect of stock size and regulations on fishing industry cost and structure: the surf clam industry. Am. J. Agr. Econ., 74: 197–208. doi.org/10.1016/j.icesjms.2004.08.016
LOESCH, J. G., and D. A. EVANS. 1994. Quantifying seasonal variation in somatic tissue: surfclam Spisula solidissima (Dillwyn, 1817) - a case study. J. Shellfish Res., 13: 425–431.
MA, H., J. P. GRASSLE, and J. M. ROSARIO. 2006. Initial recruitment and growth of surfclams (Spisula solidissima Dillwyn) on the inner continental shelf of New Jersey. J. Shellfish Res., 25: 481–489. doi.org/10.2983/0730-8000(2006)25[481:IRAGOS]2.0.CO;2
MAFMC, 1986. Amendment #6 to the Fishery Management Plan for Atlantic surfclam and ocean quahog fisheries. Mid-Atlantic Fisheries Management Council, Dover, Delaware, 102 p.
1988. Amendment #8 to the Fishery Management Plan for Atlantic surfclam and ocean quahog fisheries. Mid-Atlantic Fisheries Management Council, Dover, Delaware, 142 p.
MAHÉVAS, S., L. BELLANGER, and V. M. TRENKEL. 2008. Cluster analysis of linear model coefficients under contiguity constraints for identifying spatial and temporal fishing effort patterns. Fish. Res., 93: 29–38. doi.org/10.1016/j.fishres.2008.02.008
MAHÉVAS, S., and D. PELLETIER. 2004. ISIS-Fish, a generic and spatially explicit simulation tool for evaluating the impact of management measures on fisheries dynamics. Ecol. Modelling, 171: 65–84. doi.org/10.1016/j.ecolmodel.2003.04.001
MARZEC, R. J., Y. KIM, and E. N. Powell. 2010. Geographic trends in weight and condition index of surfclams (Spisula solidissima) in the Mid-Atlantic Bight. J. Shellfish Res., 29: 117–128. doi.org/10.2983/035.029.0104
MCCAY, B. J. 1984. The pirates of piscary: ethnohistory of illegal fishing in New Jersey. Ethnohistory, 31: 17–37. doi.org/10.2307/482021
MCCAY, B.J., S. BRANDT, and C.F. CREED. 2011. Human dimensions of climate change and fisheries in a coupled system: the Atlantic surfclam case. ICES J. Mar. Sci., 68: 1354–1367. doi.org/10.1093/icesjms/fsr044
MILLER, T. J., J. A. BLAIR, T. F. IHDE, R. M. JONES, D. H. SECOR, and M. J. WILBERG. 2010. FishSmart: an innovative role for science in stakeholder-centered approaches to fisheries management. Fisheries, 35: 424–433. doi.org/10.1577/1548-8446-35.9.422
MILLISCHER, L., and D. GASCUEL. 2006. Information transfer, behavior of vessels and fishing efficiency: an individual-based simulation approach. Aquat. Living Resour., 19: 1–13. doi.org/10.1051/alr:2006001
MONROY, C., S. SALAS, and J. BELLO-PINEDA. 2010. Dynamics of fishing gear and spatial allocation of fishing effort in a multispecies fleet. N. Am. J. Fish. Manage., 30: 1187–1202. doi.org/10.1577/M09-101.1
MYERS, R. A., K. G. BOWEN, and N. J. BARROWMAN. 1999. Maximum reproductive rate of fish at low population sizes. Can. J. Fish. Aquat. Sci., 56: 2404–2419. doi.org/10.1139/f99-201 doi.org/10.1139/cjfas-56-12-2404
MUNROE, D. M., E. N. POWELL, R. MANN, J. M. KLINCK, and E. E. HOFMANN. 2013. Underestimation of primary productivity on continental shelves: evidence from maximum size of extant surfclam (Spisula solidissima) populations. Fish. Oceanogr., 22: 220–233. doi.org/10.1111/fog.12016
NARVÁEZ, D. A., D. M. MUNROE, E. E. HOFMANN, J. M. KLINCK, E. N. POWELL, R. MANN, and E. N. CURCHITSER. 2015. Long-term dynamics in Atlantic surfclam (Spisula solidissima) populations: the role of bottom water temperature. J. Mar. Syst., 141: 136–148. doi.org/10.1016/j.jmarsys.2014.08.007
NEFSC, 1999. Fishermen’s report surfclam/ocean quahog Cape Hatteras-Gulf of Maine June 3–July 21, 1999. National Marine Fisheries Service Northeast Fisheries Science Center, Woods Hole, Massachusetts, 16 p.
2002. Fishermen’s report surfclam/ocean quahog Delmarva Peninsula-Georges Bank June 3–July 12, 2002. National Marine Fisheries Service Northeast Fisheries Science Center, Woods Hole, Massachusetts, 16 p.
2003. 37th Northeast Regional Stock Assessment Workshop (37th SAW) Stock Assessment Review Committee (SARC) consensus summary of assessments. NEFSC Ref. Doc. 03–16, 597 p.
2013. 56th Northeast Regional Stock Assessment Workshop (56th SAW) assessment report. Part A. Atlantic surfclam assessment in the US EEZ for 2013. NEFSC Ref. Doc. 13–10, 491 p.
O’LEARY, B. C., J. C. R. SMART, F. C. NEALE, J. P. HAWKINS, S. NEWMAN, A. C. MILMAN, and C. M. ROBERTS. 2011. Fisheries mismanagement. Mar. Pollut. Bull., 62: 2642–2648. doi.org/10.1016/j.marpolbul.2011.09.032
POWELL, E. N., A. J. BONNER, B. MULLER, and E. A. BOCHENEK. 2003a. Vessel time allocation in the US Illex illecebrosus fishery. Fish. Res,. 61: 35–55. doi.org/10.1016/S0165-7836(02)00245-X
POWELL, E. N., A. J. BONNER, R. MANN, and S. E. BANTA. 2003b. Evaluation of real-time catch and effort reporting in the U.S. Illex illecebrosus fishery. J. Northw. Atl. Fish. Sci., 32: 39–55. doi.org/10.2960/J.v32.a3
POWELL, E. N., J. M. KLINCK, K. ASHTON-ALCOX, E. E. HOFMANN, and J. M. MORSON. 2012. The rise and fall of Crassostrea virginica oyster reefs: the role of disease and fishing in their demise and a vignette on their management. J. Mar. Res., 70: 505–558. doi.org/10.1357/002224012802851878
RAGO, P. J., J. R. WEINBERG, and C. WEIDMAN. 2006. A spatial model to estimate gear efficiency and animal density from depletion experiments. Can. J. Fish. Aquat. Sci., 63: 2377–2388. doi.org/10.1139/f06-121
ROPES, J. W. 1968. Reproductive cycle of the surf clam, Spisula solidissima, in offshore New Jersey. Biol. Bull., 135: 349–365. doi.org/10.2307/1539787
SCAVIA, D., J. C. FIELD, D. F. BOESCH, R. W. BUDDEMEIER, V. BURKETT, D. R. CAYAN, M. FOGARTY, M. A. HARWELL, R. W. HOWARTH, C. MASON, D. J. REED, T. C. ROYER, A. H. SALLENGER, and J. G. TITUS. 2002. Climate change impacts on U.S. coastal and marine ecosystems. Estuaries, 25: 149–164. http://dx.doi.org/10.1007/BF02691304
SPRUCK, C. R., R. L. WALKER, M. L. SWEENEY, and D. H. HURLEY. 1995. Gametogenic cycle in the non-native Atlantic surf clam, Spisula solidissima (Dillwyn, 1817), cultured in the coastal waters of Georgia. Gulf Res. Rep., 9: 131–137.
WEINBERG, J. R. 1999. Age-structure, recruitment, and adult mortality in populations of the Atlantic surfclam, Spisula solidissima, from 1978–1997. Mar. Biol., 134: 113–125. http://dx.doi.org/10.1007/s002270050530
WEINBERG, J. R. 2005. Bathymetric shift in the distribution of Atlantic surfclams: response to warmer ocean temperatures. ICES J. Mar. Sci., 62: 1444–1453. http://dx.doi.org/10.1016/j.icesjms.2005.04.020
WEINBERG, J. R., T. G. DAHLGREN, and K. M. HALANYCH. 2002. Influence of rising sea temperature on commercial bivalve species of the U.S. Atlantic coast. Am. Fish. Soc. Symp., 32: 131–140.
WEINBERG, J. R., E. N. POWELL, C. PICKETT, V. A. NORDAHL JR., and L. D. JACOBSON. 2005. Results from the 2004 cooperative survey of Atlantic surfclams. NEFSC Ref. Doc., 05–01, 41 p.
WENINGER, Q., and I. E. STRAND. 2003. An empirical analysis of production distortions in the mid-Atlantic surf clam and ocean quahog fishery. Appl. Econ., 35: 1191–1197. http://dx.doi.org/10.1080/0003684032000086073
|