J. Northw. Atl. Fish. Sci., Vol. 53: 47–56
Publication (Upload) date: 13 Sep. 2022
Robertson, M.D.1* ,
, Regular, P.M.2, and Cadigan, N.1
Regular, P.M.2, and Cadigan, N.1

1Centre for Fisheries Ecosystems Research, Fisheries and Marine Institute of Memorial University of Newfoundland,
P.O. Box 4920, St. John’s, NL, A1C 5R3, Canada.
2Fisheries and Oceans Canada, Northwest Atlantic Fisheries Centre, P.O. Box 5667
80 East White Hills Rd., St. John’s, NL, A1C 5X1, Canada.
*Corresponding author. Email: matthew.robertson@mi.mun.ca
Robertson, M.D., Regular, P.M., and Cadigan, N. 2022. Limited temporal variability in natural mortality for juvenile American plaice on the Grand Bank of Newfoundland. J. Northw. Atl. Fish. Sci., 53: 47–56. https://doi.org/10.2960/J.v53.m738
Abstract
Increases in natural mortality have been suggested as a potential driver for both the collapse and lack of recovery for the American plaice (Hippoglossoides platessoides) population on the Grand Bank of Newfoundland in NAFO Divisions 3LNO. However, natural mortality is among the most difficult parameters to estimate since it can be confounded with other parameters and model misspecifications. One method used to avoid this confounding involves modeling unfished components of a population where total mortality and natural mortality are equal. Here, we use a state-space metapopulation dynamics model to investigate whether there is evidence that natural mortality rates for unfished juvenile American plaice have varied since the population collapse. In addition, our model examined the degree of synchrony in age-1 recruitment signals between each management Division. The best fitting model included temporal variability in natural mortality rates, but estimates did not frequently differ from zero. This indicates that change in natural mortality rates is not an important driver of current juvenile 3LNO American plaice stock dynamics. Instead, this model identified that juvenile stock dynamics were mainly affected by variations in age-1 recruitment. Furthermore, a correlation analysis of the temporal variations in recruitment showed that trends were somewhat dissimilar between NAFO Divisions 3L and 3NO. Overall, although increases in M have been suggested by recent studies, we did not find strong evidence for this in juvenile fish.
Keywords: cohort dynamics, population dynamics, recruitment, spatiotemporal, state-space models
PDF | Suppl. material
Download Citation Data

Citation to clipboard
 Reference management software (Endnote, Mendeley, RefWords, Zotero & most other reference management software)
Reference management software (Endnote, Mendeley, RefWords, Zotero & most other reference management software)
LaTex, BibDesk & other specific software
Introduction
Increases in natural mortality rates (M’s) have been suggested as a potential driver for both the collapse and lack of recovery for the American plaice (Hippoglossoides platessoides) population on the Grand Bank of Newfoundland in NAFO Divisions 3LNO (Morgan and Brodie, 2001; COSEWIC, 2009; Morgan et al., 2011; Perreault et al., 2020). In fact, in the most recent run of the ADAPT model for this stock (Wheeland et al., 2021) and in previously accepted models (e.g. Wheeland et al., 2018), the assumed M was increased from 0.2 to 0.53 for all ages from 1989 to 1996. In the late 1980s – early 1990s 3LNO American plaice collapsed, and despite a moratorium on directed commercial fishing since 1994, the population has yet to recover (Fig. 1; Wheeland et al., 2021). Despite an expectation that the collapse and lack of recovery were mainly driven by overfishing (directed fishing for the collapse, and bycatch for the lack of recovery), population dynamics models have indicated that known catches are unlikely to account for observed increases in total mortality rates (Z) both during and after the collapse (Morgan and Brodie, 2001; Perreault et al., 2020). Such increases in Z have consequently been, at least partially, attributed to shifts in M. These shifts are hypothesized to be linked to particularly low bottom-water temperatures that covered the Grand Bank during this time-period (Morgan, 1992; Walsh et al., 2004; Robertson et al., 2021); however, direct estimation of the temporal variability in M and its drivers has yet to occur.
Although M is often considered to be one of the most important parameters in a fish stock assessment model, it is also among the most difficult parameters to estimate using commonly available data (Punt et al., 2021). It can be confounded with survey gear selectivity and fishing mortality rates (Pope et al., 2021). Even when M can be estimated numerically, it may be confounded or aliased with other model misspecifications and M estimates may then be unreliable. There are two main methods capable of avoiding the confounding issue. The first is integration of additional data that can inform M estimates. This usually involves tagging data (e.g. Pine, Pollock, Hightower, Kwak, and Rice, 2003; Cadigan, 2015), but there are recent examples that used fish condition indices (e.g. Regular et al., 2022). Another approach involves examinations of unfished components of a population (Myers and Cadigan, 1993a, 1993b; Gudmundsson, 2004; Zhang et al., 2020). Although 3LNO American plaice lack a time-series of mark-recapture data (but see Morgan (1996) for a tagging experiment), this stock benefits from having research surveys that catch a wide range of ages, including juvenile age-classes (ages 1–5) that are too small to be captured by the fishery. Survey indices of these age-classes provide a means to examine trends in M for the juvenile component of this population since their Z and M should be equal.
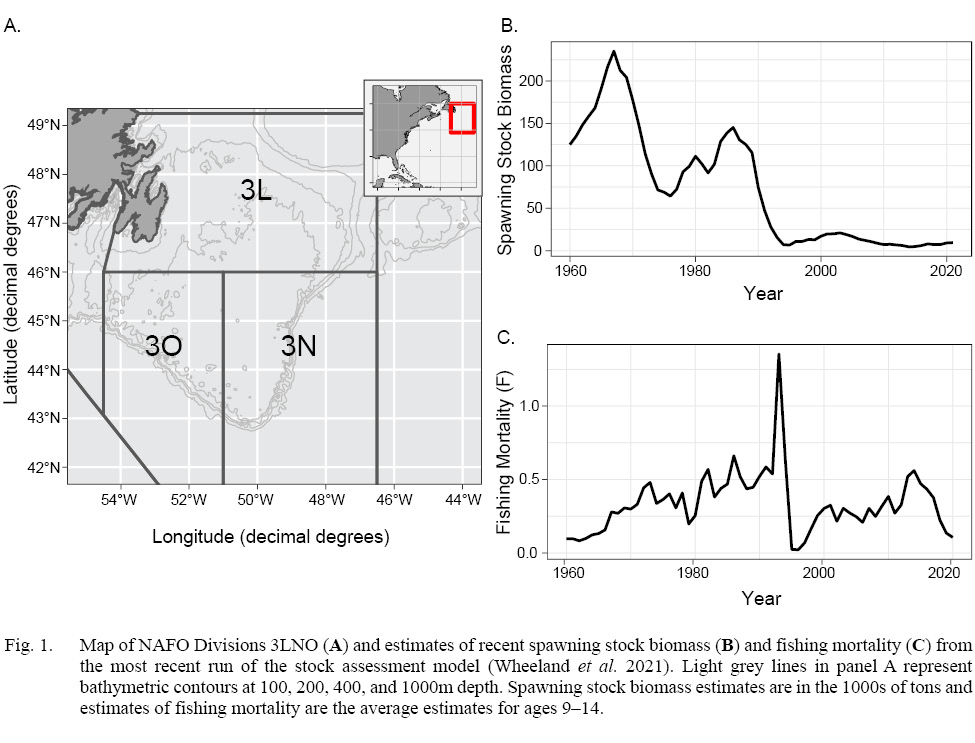
Fig. 1
Here we use a state-space metapopulation dynamics model to investigate whether there is evidence that American plaice juvenile M has varied since the population collapse. This model is applied to juvenile (ages 1–5) abundance indices on the Newfoundland Grand Bank since 1995. American plaice have spatiotemporally varying, sexually dimorphic growth with juveniles growing from approximately 5 to 20cm, female maturation occurring around age eight, and male maturation occurring around age four in recent years in NAFO divisions 3LNO (Zheng et al., 2020a, 2020b). A previous use of this model assessed juvenile cod M around Newfoundland and Labrador, where both cohort strength and M were found to vary across space and time (Zhang et al., 2020). Here, we limited our analysis to one stock on the Grand Bank, but allowed for separate estimates in each management division due to previous findings of divisional-level recruitment asynchrony (Kumar et al., 2019).
Materials and Methods
Metapopulation dynamics process model
The model used here was developed by Zhang et al. (2020) and a more detailed description can be found there. Briefly, this model framework uses age-based survey indices of unfished juvenile fish abundance to estimate changes in juvenile M and cohort strength within metapopulation units. The model is based on the common cohort population model, Na,y=Na-1,y-1exp(-Ma-1,y-1), where Na,y represents stock abundance at age a in year y and Ma,y is the natural mortality rate. We assume that Ma,y can be modelled in terms of age- and year-effects, Ma,y=Ma+δy, where Ma (a = 0,…,A) is the overall level of juvenile mortality at age a and δy (y =0,…,Y) is the annual deviation Ma,y-Ma that we assume is common for all juvenile ages. If c = y - a indicates the cohort and na,y=logNa,y, then we can show through recursive applications of the basic cohort model that
na,c=n0,c-∑i=0a-1Mi+δc+i, a>0.(1)
We model δy for y=1,…,Y using a stationary Gaussian autoregressive process with a correlation parameter φδ and stationary variance σδ2/(1-φδ2):
δ0~N0, σδ21-φδ2, δy|δy-1 ~ Nφδδy-1,σδ2 , y=1,…,Y(2)
Note that δy|δy-1 denotes the distribution of δy conditional on the value δy-1, and σδ2=Varδyδy-1≤ Varδy.
In addition, we model the time-series of the initial cohort abundance (n0,c; i.e. recruits) using an intercept plus a Gaussian autoregressive cohort effect (γc),
n0,c=n0+γc,(3)
where
γ0 ~N0, σγ21-φγ2, γc|γc-1 ~ Nφγγc-1,σγ2 , c=1,…,C(4)
Observation model
Our model is based on bottom trawl research survey indices Is,a,y, where s denotes the survey, a denotes the age, and y denotes the year. Each age-class in the surveys is expected to have unique catchability Qs,a which is based on gear selectivity and availability of fish at different ages (and sizes) to the survey. Our basic observation model is
Is,a,y≈Qs,aNs,a,yexp-fsMs,a+δs,y,
where fs is the fraction of the year that survey s occurs and the exp-fsMs,a+δs,y term simply projects beginning of year abundance (Ns,a,y) to the survivors at the time of the survey. We collect all of the M deviations and cohort abundance random effects into the set
Ψ=δy,γc;y=1,…,Y,c=1,…,C. Let qs,a=logQs,a and define μs,a,y=ElogIs,a,y|Ψ to be the statistical expected value of logIs,a,y given all the random effects. The expectations are
|
μs,a=0,y=c=qs,0*+ns,0,c-fsδs,c,
|
(5)
|
and
|
μs,a,y=c+a=qs,a*+ns,0,c-∑i=0a-1δs,c+i-fsδs,c+a, a>0,
|
(6)
|
where qs,0*=qs,0-fsMs,0 and qs,a*=qs,a- ∑i=0a-1Ms,i-fsMs,a. As described in Zhang et al. (2020), the qs,a and Ms,a values are completely confounded, therefore we cannot directly estimate Ms,a without additional information on qs,a. As a result, we estimate their combined effect, qs,a*.
The survey index observation equation is
|
logIs,a,y= μs,a,y+τs,y+ εs,a,y,
|
(7)
|
where τs,y and εs,a,c are normally distributed 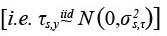 survey measurement errors. The random year-effects (τs,y) allow for measurement errors to be correlated across ages within surveys and years, which is common for survey indices of juvenile ages. However, these errors are independent for different years and surveys. Due to this structure, these year-effects will only affect estimates in a particular year, rather than having a cumulative effect on cohort dynamics like the temporal deviations in M. Furthermore, qs,a=5* is constrained to be zero for each survey to eliminate the confounding between the values of qs,a* and ns,0,c in Equation (6). Finally, we estimate between-survey and unstructured correlations in both Ms,a.y and ns,0,c, which is described in Zhang et al. (2020). These correlations represent the metapopulation aspect of the model, where population processes may be similar among NAFO divisions. These correlations were examined with a hierarchical cluster analysis using the `hclust` function in R on the Pearson dissimilarity between surveys.
survey measurement errors. The random year-effects (τs,y) allow for measurement errors to be correlated across ages within surveys and years, which is common for survey indices of juvenile ages. However, these errors are independent for different years and surveys. Due to this structure, these year-effects will only affect estimates in a particular year, rather than having a cumulative effect on cohort dynamics like the temporal deviations in M. Furthermore, qs,a=5* is constrained to be zero for each survey to eliminate the confounding between the values of qs,a* and ns,0,c in Equation (6). Finally, we estimate between-survey and unstructured correlations in both Ms,a.y and ns,0,c, which is described in Zhang et al. (2020). These correlations represent the metapopulation aspect of the model, where population processes may be similar among NAFO divisions. These correlations were examined with a hierarchical cluster analysis using the `hclust` function in R on the Pearson dissimilarity between surveys.
Data
We used six relative abundance indices of juvenile (ages 1–5) American plaice from stratified random research bottom-trawl surveys in NAFO Divisions 3LNO. These surveys were conducted in the spring (~April–June) and fall (~ October–November) and were separated based on NAFO Divisions (i.e. spring 3L, spring 3N, spring, 3O, fall 3L, fall 3N, and fall 3O). We limited the time-series for our analysis to spring surveys conducted after 1996 and fall surveys after 1995 due to low catchability of age 1 American plaice with the bottom trawl gear used in prior years (Morgan et al., 1998). Surveys were not completed in some years and any indices with zero or very small values (i.e. <e-5) were not used; see SM. Fig. 1).
Model fitting
We examined thirteen parameterizations of the model, with varying numbers of random effects (γc, τs,y, δc) to determine which components were necessary to account for the variability in the sampled survey indices (Table 1). In addition to sequentially adding components, we tested various correlation structures to identify if cohort effects or M deviations varied across space and season. Model selection was completed using a combination of Akaike’s information criterion (AIC), Bayesian information criterion (BIC), and examinations of residuals. BIC measures goodness-of-fit, while AIC is a measure of prediction accuracy (Sober, 2002). We used the Template Model Builder (TMB, Kristensen et al., 2016) package in R (R Core Team, 2018) to evaluate the negative logarithms of the marginal likelihoods (nll) of these models and the data, and to evaluate the nll gradients to improve estimation. Further, we used the R function nlminb() to find the maximum likelihood estimates. Model convergence was evaluated by ensuring that the nll gradient for all parameters was <10-4 and that the Hessian matrix was positive definite at the maximum-likelihood estimates.
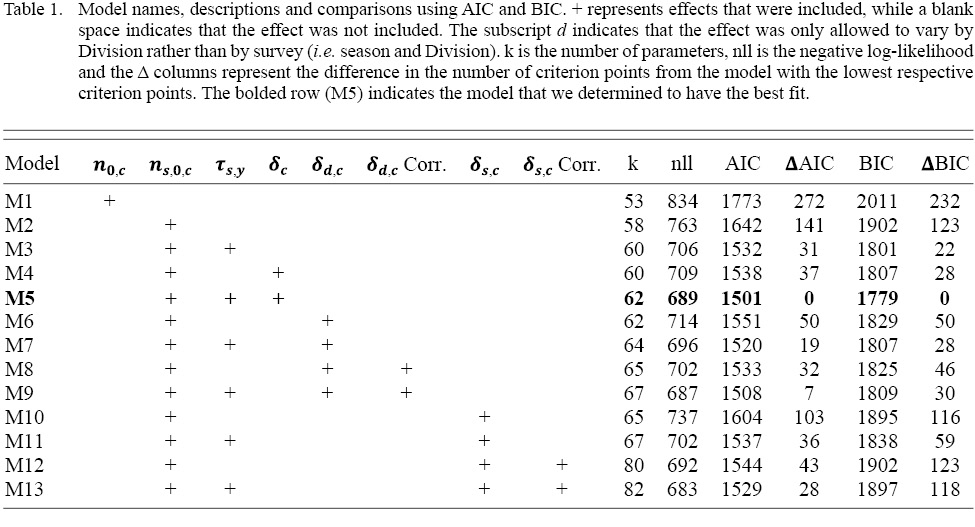
Table 1
Results
Our model comparisons indicated that the model with the best fit was model M5 which had cohort and year-effects, as well as M deviations that were shared across Divisions (Table 1). Model M5 fit the data well, with no observable trends in residual plots (see SM. Figs. 6–16). This model was an improvement over the simpler model M4, and had no survey year-effects in standardized residuals (SM. Figs. 2 and 3). M4 had clear residual year-effects (SM. Fig. 2) that were substantially reduced in M5, although a similar trend of small magnitude remained (SM. Fig. 3). M5 included spatial and temporal variability in cohort effects (Fig. 2). Despite 3LNO being managed as a single stock, our model selection process showed substantial improvements in estimates when cohort effects were allowed to vary by Division and season (Table 1). The temporal trends indicated that in NAFO Division 3L, cohort effects decreased until 1996, increased after this until 2012, and have since declined somewhat steadily. Meanwhile, there was much less of a trend in NAFO Divisions 3NO, where cohort effects generally oscillated around a mean with a period of around 5–6 years. The similarity in cohort effect trends between 3N and 3O was identified in the spatial cohort effect correlation matrix (Fig. 3) where 3N and 3O surveys always had a high correlation with each another (>0.9). Meanwhile, the correlations between cohort strength derived from 3L surveys and those in 3N and 3O were often lower (≤0.5). This was further illustrated using a cluster analysis that identified that the cohort effects for 3NO were dissimilar from the cohort effects for 3L (Fig. 4).
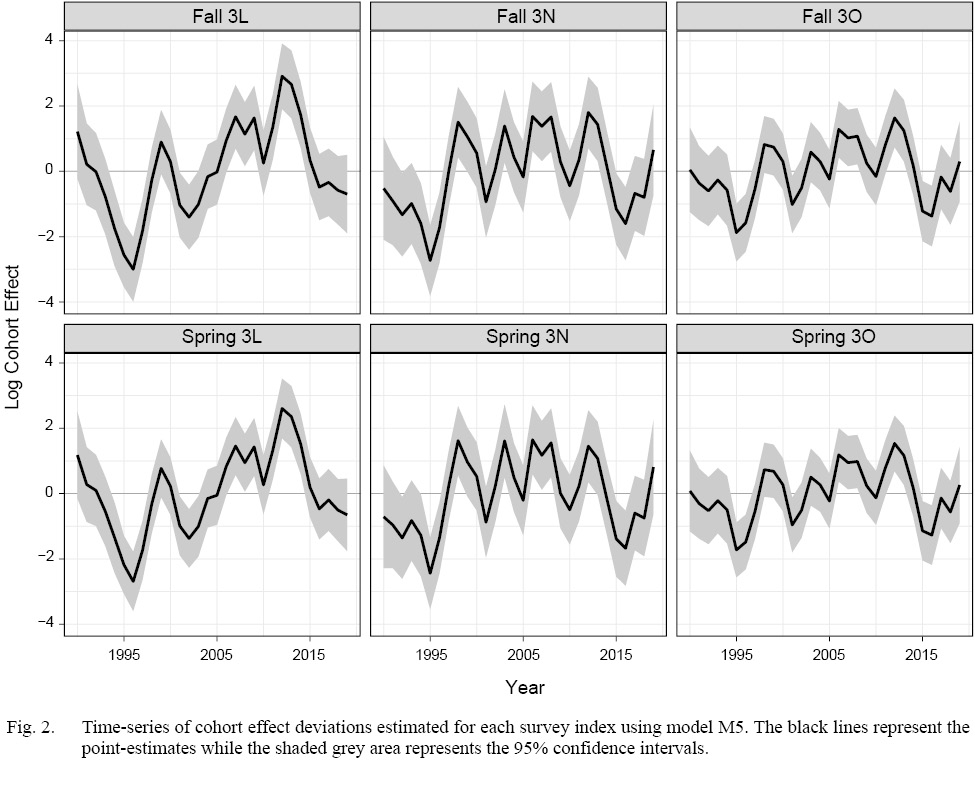
Fig. 2
Model M5 indicated that accounting for M deviations was necessary to produce the best fits to the survey indices. M5 had the simplest formulation of M deviations, where they were assumed to be equal across NAFO Divisions 3LNO (Table 1). Therefore, unlike cohort effects, our results indicate that M deviations may not vary by Division or season and may be driven by a larger scale process. Finally, despite improving model fit, the estimates of M deviations only differed significantly from zero in four years: 1999, 2005, 2015, and 2016 (Fig. 5). At the extreme, the estimates suggest M’s in 2015–16 were slightly more than double those in 1999–2000. Estimated changes in M were much smaller in other years.
Discussion
We applied a state-space metapopulation dynamics model to identify whether American plaice juvenile natural mortality rates (M’s) have affected stock dynamics since the population collapse. Our model comparison identified that estimating temporal variability in M improved the model fit to juvenile 3LNO American plaice survey indices which indicates that temporal variability in M may influence the dynamics of the unfished portion of the stock. The best fitting model included spatial cohort and survey year-effects, along with non-spatial M deviations. Although this best fitting model included temporal M deviations, estimates were rarely significantly different from zero. The limited variation in these M deviations in comparison to the larger magnitude variations in age-1 recruitment indicated that juvenile stock dynamics were mainly affected by recruitment. Furthermore, temporal variations in cohort effects were more dissimilar between NAFO Divisions 3L and 3NO, implying that drivers of age-1 recruitment may differ between these regions.
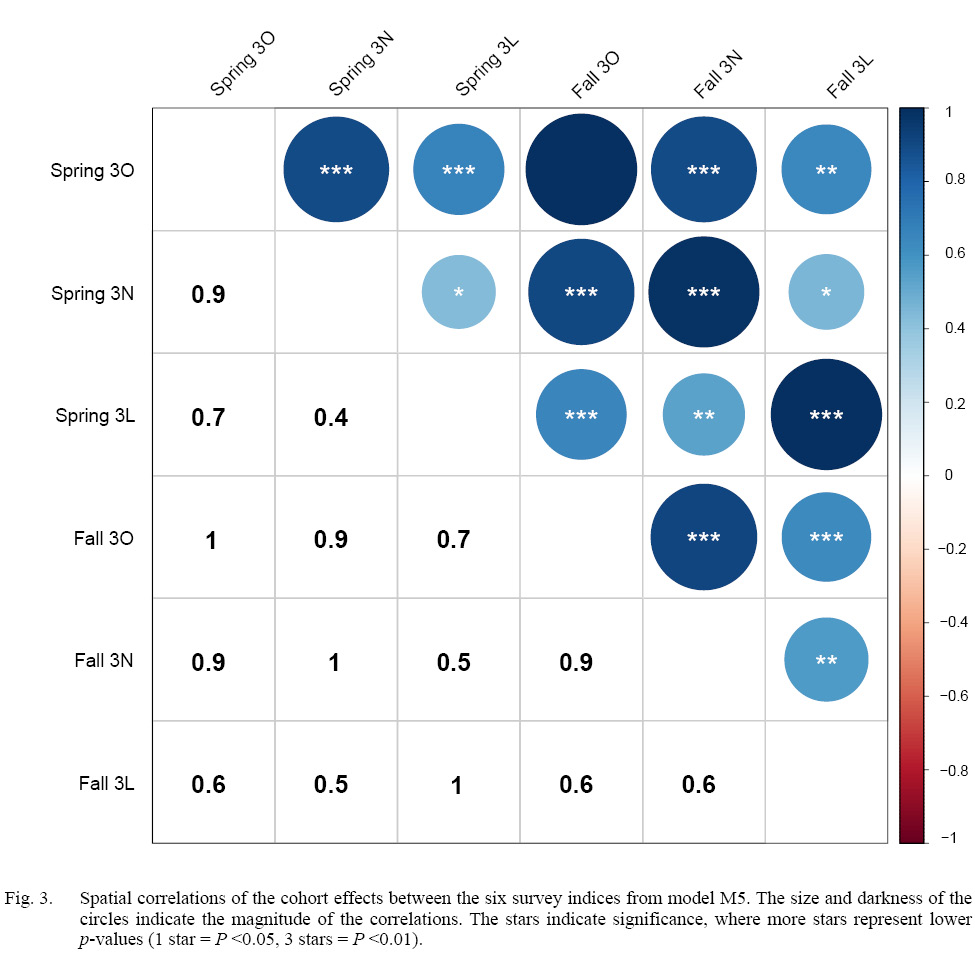
Fig. 3
Recent analyses have indicated that current assumptions about M in 3LNO American plaice stock assessments underestimate its impact on the slow recovery for this stock (Perreault et al., 2020; Wheeland, 2021). Here, we observed that estimating temporal variability in juvenile M improved estimates of juvenile stock dynamics. However, annual M deviations were rarely significantly different from zero, indicating that the variation is less important compared to spatial and temporal variations in cohort strength. This finding matches results from a previous cohort model used for this stock that assessed the potential for changes in M graphically rather than modelling it as we have done here (Kumar et al., 2019). Furthermore, this finding matches broader findings that demersal fish juvenile natural mortality tends to show limited temporal variability (Myers and Cadigan, 1993a; Gudmundsson, 2004). The limited variability in juvenile M may affect our ability to understand the drivers of current stock assessment problems for this stock. For example, our findings differ from a recent exploration of M deviations where there was an indication that accounting for temporal change in M at young ages would help reduce retrospective patterns (Perreault et al., 2020). This difference in magnitude of influence of natural mortality may have been generated by M deviations at young ages producing better fits by reducing recruitment variance since the Perreault et al. (2020) model formulation did not include an M deviation variance penalty like the model employed here. Overall, although increases in M have been suggested by recent studies, we did not find strong evidence for this in juvenile fish.
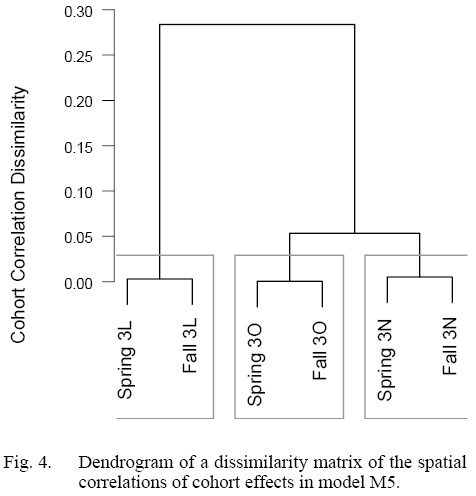
Fig. 4
We did not find evidence of large changes in juvenile M since the fishing moratorium in 1995, but this does not mean that high juvenile M is not a factor in the delayed recovery of the stock. It is possible that recent M’s are much higher than those prior to 1995. However, our model and the available survey data only allow the estimation of M deviations, which cannot inform the magnitude of M to provide any direct indication of whether current M is high relative to expected levels of juvenile M. As a result, investigating how juvenile M has varied pre- and post-collapse would require a longer historical time series. Since fall survey indices are only available since 1990, they cannot provide much information about pre-collapse M. Spring survey indices go back to 1985, but the survey trawl used in the Spring during 1985–1995 had a larger mesh size than the current trawl and indices for age 1–2 seem less reliable. They include many zeroes that we cannot use in the current model formulation. Although Spring indices at ages 3–5 are more reliable, it would be difficult to differentiate between a change in M and year-effects with survey indices for only three ages. Hence, extending our model back to the mid-1980s does not seem useful. Our juvenile metapopulation dynamics model is only practically useful with indices produced by surveys that are effective at monitoring juveniles, such as the current DFO bottom trawl surveys that use the Campelen trawl.
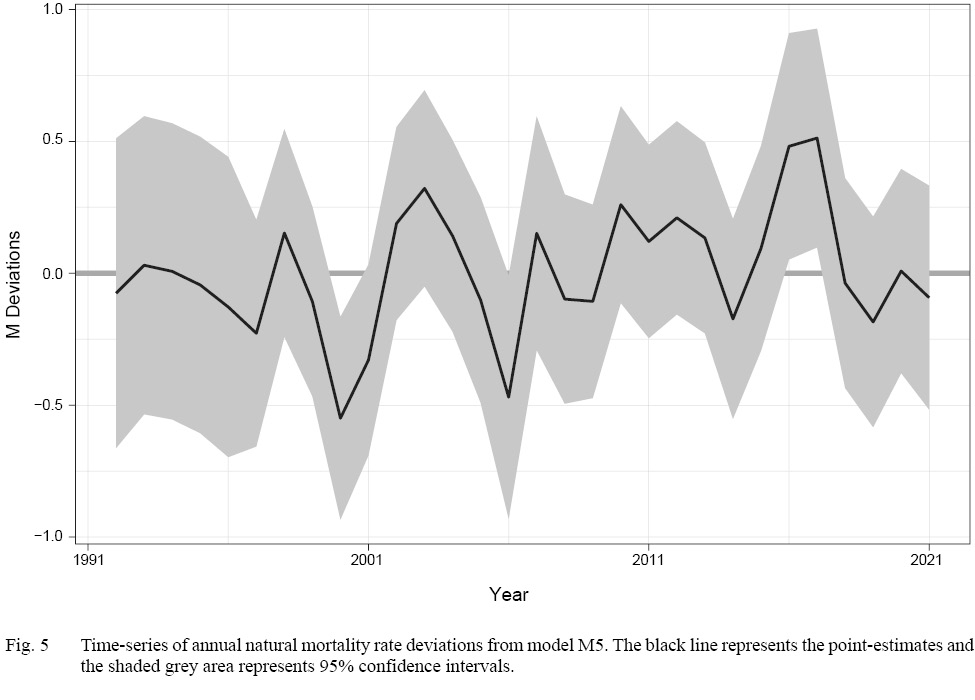
Fig. 5
Unlike the cohort effect, there was little evidence of differences in juvenile M across NAFO Divisions, indicating that the main driver(s) of mortality is likely a large scale process. Large-scale processes affecting juvenile M could include bottom-up processes like bottom-water temperature or prey availability, or top-down processes like predation or competition. Regardless of the particular driver, it is interesting that the spatiotemporal structure of M and age-1 recruitment (e.g. cohort effects) differed. Although differences in the spatial scales affecting different aspects of population dynamics are likely inherent in many populations (i.e. Levin 1992) recognizing these differences can produce an improved mechanistic understanding of the observed patterns.
The cohort strength effects for juvenile 3LNO American plaice are much larger than the effects of time-varying M. This finding is not particularly novel since understanding recruitment dynamics has been at the core of fisheries science for over a century due to its large influence on population dynamics (e.g., Houde, 2008). However, in a recent analysis of juvenile Atlantic cod dynamics around Newfoundland and Labrador, oscillations with a similar period to those estimated here were identified in both M deviations and cohort effects (Zhang et al., 2020). Furthermore, these oscillations are similar to estimates of weight-at-length (an indicator of condition and potentially starvation induced mortality) for 3Ps Atlantic cod (Cadigan et al., 2022). The 3Ps Atlantic cod model estimates were compared to regional drivers and significant correlations were identified for oceanographic (e.g. bottom water temperature), basal food web (e.g. zooplankton), and direct prey abundance (3LNO Northern sand lance (Ammodytes dubius)). Therefore, it is possible that Atlantic cod and American plaice recruitment and/or M are affected by similar environmental and/or trophic mechanisms.
In addition to the influence of age-1 recruitment, we also observed a substantial influence of survey year-effects on model estimates. Survey year-effects are used to account for correlated observation error among ages in a particular survey that can occur for a variety of unknown reasons (Myers and Cadigan, 1995). For example, catchability may vary annually depending on environmental conditions, there may be anomalous sets accounting for a majority of catch, or there could be differences in how survey crew handles the fishing gear. Additionally, the survey year-effects may be necessary to account for stock distributional shifts (Swain and Sinclair, 1994; Swain and Benoit, 2003). Accounting for these year-effects is important when modelling juvenile dynamics based on survey indices; however, their source(s) remains speculative.
There is substantial evidence that M varies with body size and age, often by orders of magnitude over the life cycle (Lorenzen et al., 2022). Although our metapopulation dynamics model was based on separate age-dependent M’s for each metapopulation, we assumed that annual deviations in M were the same for all ages even though the absolute value of M could differ substantially among ages. Yet, this simplifying assumption may be unrealistic. For example, if M at age 1 is 2.0 and M at age 5 is 0.3 then it is possible that annual M deviations at age two are larger than at age five. However, additive M deviations have a multiplicative effect on cohort survival; that is, if then Na+1,y+1=Na-1,y-1exp(-Ma)exp(-δy-1). If annual M deviations are multiplicative in nature then a more realistic M model would be Ma,y=Maexp(δy) or logMa,y=logMa+δy (Cadigan, 2015; Stock and Miller, 2021). Using the approximation expδy≈1+δy, then . Note that if δy is normally distributed with mean zero and stationary variance σδ2/(1-φδ2) then also is also normally distributed with mean zero but with stationary variance 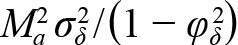 . As a result, the necessity for using multiplicative rather than additive M deviations for a population where Ma decreases with age could be explored by examining whether there is higher residual variation at younger ages in an additive M deviation model. This is exactly the pattern we found (see SM. Fig. 4). However, it is also possible that the εs,a,c survey measurement error variances (see Equation 7) are higher at younger ages, which is another possible model misspecification. The within-survey variance of the indices may indicate if the patterns in SM. Fig. 4 are consistent with sampling variability or not, but these sampling variances were not available to us. Therefore, given the current data, these effects are confounded and we cannot identify whether the observed residual variance pattern is the result of process or observation error. Finally, implementing a model with multiplicative M deviations would also require that we specify the age pattern in M’s. However, we are unsure why the residual variation in SM. Fig. 4 usually increases at age five but sometimes at age four. These are areas that require further research.
. As a result, the necessity for using multiplicative rather than additive M deviations for a population where Ma decreases with age could be explored by examining whether there is higher residual variation at younger ages in an additive M deviation model. This is exactly the pattern we found (see SM. Fig. 4). However, it is also possible that the εs,a,c survey measurement error variances (see Equation 7) are higher at younger ages, which is another possible model misspecification. The within-survey variance of the indices may indicate if the patterns in SM. Fig. 4 are consistent with sampling variability or not, but these sampling variances were not available to us. Therefore, given the current data, these effects are confounded and we cannot identify whether the observed residual variance pattern is the result of process or observation error. Finally, implementing a model with multiplicative M deviations would also require that we specify the age pattern in M’s. However, we are unsure why the residual variation in SM. Fig. 4 usually increases at age five but sometimes at age four. These are areas that require further research.
We identified that the recruitment trends appear to differ between NAFO Divisions 3L and 3NO despite these management Divisions comprising the same stock. Similar results were found in a different cohort model used for American plaice stocks throughout all of Newfoundland and Labrador (NAFO Divisions 2J3KLNOPs; Kumar et al., 2019). The spatial extent of management on the Grand Bank varies by species. Yellowtail flounder and American plaice are the only two species whose management occurs across NAFO Divisions 3LNO, whereas other species are managed separately between 3L and 3NO (e.g. 2J3KL vs. 3NO Atlantic cod). Previous studies have argued that American plaice in NAFO Division 3L differ from those in 3NO (see review by Brodie, 2002). These arguments have stemmed from various lines of evidence including differences in growth and maturity (Zheng et al., 2020b), in divisional research surveys indicating different trends in abundance, and as a result of the general sedentary nature of American plaice in this region (Pitt,1969; Morgan, 1996). Since incorrect delineation of stock spatial structure can affect estimates of productivity and in turn affect management decision-making (e.g. Kerr et al., 2017), further work on addressing this question for 3LNO American plaice is warranted.
Acknowledgements
Research funding to N.C. and M.D.R. was provided by the Ocean Frontier Institute, through an award from the Canada First Research Excellence Fund. Research funding to M.D.R was provided by the Vanier Canada Graduate Scholarship. Research funding to N.C. was provided by the Ocean Choice International Industry Research Chair program at the Marine Institute of Memorial University of Newfoundland. We also thank the Northwest Atlantic Fisheries Centre, Fisheries and Oceans Canada, the many people involved in the collection and processing of these data.
References
Brodie, W. B. 2002. American Plaice Hippoglossoides platessoides on the Grand Bank (NAFO Divisions 3LNO) – a Review of Stock Structure in Relation to Assessment of the Stock.
Cadigan, N. G. 2015. A state-space stock assessment model for northern cod, including under-reported catches and variable natural mortality rates. Can. J. Fish. Aquat. Sci. 73(2): 296–308. https://doi.org/10.1139/cjfas-2015-0047
Cadigan, N. G., Robertson, M. D., Nirmalkanna, K., and Zheng, N. 2022. The complex relationship between weight and length of Atlantic cod off the south coast of Newfoundland. Can. J. Fish. Aquat. Sci.: 1–33. https://doi.org/10.1139/cjfas-2021-0325.
COSEWIC. 2009. COSEWIC assessment and status report on the American Plaice Hippoglossoides platessoides, Maritime population, Newfoundland and Labrador population and Arctic population, in Canada. Ottawa.
Gudmundsson, G. 2004. Time-series analysis of abundance indices of young fish. ICES J. Mar. Sci. 61: 176–183. https://doi.org/10.1016/j.icesjms.2003.12.001
Houde, E. D. 2008. Emerging from Hjort’s shadow. J. Northwest Atl. Fish. Sci. 41: 53–70. https://doi.org/10.2960/J.v41.m634.
Kerr, L. A., Hintzen, N. T., Cadrin, S. X., Clausen, L. W., Dickey-collas, M., Goethel, D. R., Hatfield, E. M. C., Kritzer, J. P., and Nash, R. D. M. 2017. Lessons learned from practical approaches to reconcile mismatches between biological population structure and stock units of marine fish. ICES J. Mar. Sci. 74(6): 1708–1722. https://doi.org/10.1093/icesjms/fsw188.
Kristensen, K., Nielsen, A., Berg, C. W., Skaug, H., and Bell, B. 2016. TMB: Automatic Differentiation and Laplace Approximation. J. Stat. Softw. 70(5): 21. https://doi.org/10.18637/jss.v070.i05.
Kumar, R., Cadigan, N.G., and Morgan, M. J. 2019. Recruitment synchrony in spatially structured Newfoundland and Labrador populations of American plaice (Hippoglossoides platessoides). Fish. Res. 211(May 2018): 91–99. Elsevier. https://doi.org/10.1016/j.fishres.2018.10.027.
Levin, S. 1992. The problem of pattern and scale in ecology. Ecology, 73(6): 1943–1967. https://doi.org/10.2307/1941447.
Lorenzen, K., Camp, E. V, and Garlock, T. M. 2022. Natural mortality and body size in fish populations. Fish. Res. 252: 106327. Elsevier B.V. https://doi.org/10.1016/j.fishres.2022.106327
Morgan, M., and Brodie, W. 2001. An Exploration of Virtual Population Analyses for Divisions 3LNO American Plaice. NAFO SCR Doc., No. 4, Serial No. 4368, 20 p.
Morgan, M., Brodie, W., Bowering, W., Maddock Parsons, D., and Orr, D. 1998. Results of Data Conversions for American Plaice in Div. 3LNO from Comparative Fishing Trials Between the Engel Otter Trawl and the Campelen 1800 Shrimp Trawl. NAFO SCR Doc., No. 70, Serial No. 3062, 10 p.
Morgan, M. J. 1992. Low-Temperature Tolerance of American Plaice in Relation to Declines in Abundance. Trans. Am. Fish. Soc. 121: 399–402. https://doi.org/10.1577/1548-8659(1992)121%3C0399:LTOAPI%3E2.3.CO;2
Morgan, M. J. 1996. Preliminary results of tagging experiments on American plaice in NAFO Divs. 3LNO. NAFO SCR Doc., No. 61, Serial No. 2737, 13 p.
Morgan, M. J., Bailey, J., Healey, B. P., Maddock Parsons, D., and Rideout, R. 2011. Recovery potential assessment of American Plaice (Hippoglossoides platessoides) in Newfoundland and Labrador. DFO Can. Sci. Advis. Sec. Res. Doc. 2011/047.
Myers, R. A., and Cadigan, N. C. 1993a. Is juvenile natural mortality in marine demersal fish variable? Can. J. Fish. Aquat. Sci. 50: 1591–1598. https://doi.org/10.1139/f93-180
1993b. Density-dependent juvenile mortality in marine demersal fish. Can. J. Fish. Aquat. Sci. 50: 1576–1590. https://doi.org/10.1139/f93-179
1995. Statistical-Analysis of Catch-at-Age Data with Correlated Errors. Can. J. Fish. Aquat. Sci. 52(6): 1265–1273. https://doi.org/10.1139/f95-123.
Perreault, A. M. J., Wheeland, L. J., and Morgan, M. J. 2020. A state-space stock assessment model for American plaice on the Grand Bank of Newfoundland. J. Northwest Atl. Fish. Sci. 51: 45–104. https://doi.org/10.2960/J.v51.m727
Pine, W. E., Pollock, K. H., Hightower, J. E., Kwak, T. J., and Rice, J. A. 2003. A review of tagging methods for estimating fish population size and components of mortality. Fisheries, 28(10): 10–23. https://doi.org/10.1577/1548-8446(2003)28[10:AROTMF]2.0.CO;2
Pitt, T. K. 1969. Migrations of American Plaice on the Grand Bank and in St. Mary’s Bay, 1954, 1959, and 1961. J. Fish. Res. Board Canada 26: 1301–1319. https://doi.org/10.1139/f69-115
Pope, J. G., Gislason, H., Rice, J. C., and Daan, N. 2021. Scrabbling around for understanding of natural mortality. Fish. Res. 240: 105952. Elsevier B.V. https://doi.org/10.1016/j.fishres.2021.105952
Punt, A. E., Castillo-Jordan, C., Hamel, O. S., Cope, J. M., Maunder, M. N., and Ianelli, J. N. 2021. Consequences of error in natural mortality and its estimation in stock assessment models. Fish. Res., 233: 105759. https://doi.org/10.1016/j.fishres.2020.105759
R Core Team. 2018. R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. Available from https://www.r-project.org/.
Regular, P. M., Buren, A. D., Dwyer, K. S., Cadigan, N. G., Gregory, R. S., Koen-alonso, M., Rideout, R. M., Robertson, G. J., Robertson, M. D., Stenson, G. B., Wheeland, L. J., and Zhang, F. 2022. Indexing starvation mortality to assess its role in the population regulation of Northern cod. Fish. Res., 247: 106180. Elsevier B.V. https://doi.org/10.1016/j.fishres.2021.106180
Robertson, M. D., Gao, J., Regular, P. M., Morgan, M. J., and Zhang, F. 2021. Lagged recovery of fish spatial distributions following a cold - water perturbation. Sci. Rep.: 1–11. Nature Publishing Group UK. https://doi.org/10.1038/s41598-021-89066-x
Sober, E. 2002. Instrumentalism, parsimony, and the Akaike framework. Philosophy of Science, 69(S3), S112-S123. https://doi.org/10.1086/341839
Stock, B. C., and Miller, T. J. 2021. The Woods Hole Assessment Model (WHAM): A general state-space assessment framework that incorporates time- and age-varying processes via random effects and links to environmental covariates. Fish. Res., 240(105967). Elsevier B.V. https://doi.org/10.1016/j.fishres.2021.105967.
Swain, D. P., and Benoit, H. P. 2003. Accounting for length- and depth-dependent diel variation in catchability of fish and invertebrates in an annual bottom-trawl survey. ICES J. Mar. Sci., 60: 1298–1317. https://doi.org/10.1016/S1054-3139(03)00124-3
Swain, D. P., and Sinclair, A. F. 1994. Distribution and Catchability: What is the Appropriate Measure of Distribution? Can. J. Fish. Aquat. Sci., 51: 1046–1054. https://doi.org/10.1139/f94-104
Walsh, S. J., Simpson, M., and Morgan, M. J. 2004. Continental shelf nurseries and recruitment variability in American plaice and yellowtail flounder on the Grand Bank: Insights into stock resiliency. J. Sea Res., 51(3–4): 271–286. https://doi.org/10.1016/j.seares.2003.10.003
Wheeland, L. 2021. An exploration of the impact of natural mortality assumptions in a Virtual Population Analysis for Divisions 3LNO American Plaice. NAFO SCR Doc., No. 025, Serial No. 7193, 16 p.
Wheeland, L., Dwyer, K., Kumar, R., Rideout, R., Perreault, A., and Rogers, B. 2021. Assessment of American plaice in Div. 3LNO. NAFO SCR Doc., No. 035, Serial No. 7204, 63 p.
Wheeland, L., Dwyer, K., Morgan, J., Rideout, R., and Rogers, R. 2018. Assessment of American Plaice in Div. 3LNO. NAFO SCS Doc., No. 039, Serial No. N6829, 77 p.
Zhang, F., Rideout, R., and Cadigan, N. 2020. Spatiotemporal variations in juvenile mortality and cohort strength of Atlantic cod (Gadus morhua) off Newfoundland and Labrador. Can. J. Fish. Aquat. Sci., 77(3): 625–635. https://doi.org/10.1139/cjfas-2019-0156
Zheng, N., Cadigan, N. G., and Morgan, M. 2020a. A spatiotemporal Richards–Schnute growth model and its estimation when data are collected through length-stratified sampling. Environ. Ecol. Stat., 27(3): 415–446. https://doi.org/10.1007/s10651-020-00450-8
Zheng, N., Robertson, M., Cadigan, N., Zhang, F., Morgan, J., and Wheeland, L. 2020b. Spatiotemporal variation in maturation : A case study with American plaice (Hippoglossoides platessoides) on the Grand Bank off Newfoundland. Can. J. Fish. Aquat. Sci., 77(10): 1688–1699. https://doi.org/10.1139/cjfas-2020-0017
Citation: Robertson, M.D., Regular, P.M., and Cadigan, N. 2022. Limited temporal variability in natural mortality for juvenile American plaice on the Grand Bank of Newfoundland. J. Northw. Atl. Fish. Sci., 53: 47–56. https://doi.org/10.2960/J.v53.m738